Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 10.Problemas - Ex. 1
No problema do degrau de potencial (Seç. 10.2), mostre que não podem existir estados estacionários com
Sugestão: Escreva as soluções nas regiões 1 e 2 e mostre que não é possível satisfazer as condições de contorno em .
Passo 1
Para resolvermos esse problema, vamos precisar escrever as equações para as duas regiões, como dito na sugestão, e aplicar a condição de contorno em . Vamos analisar as equações de acordo com a energia disponível em relação ao potencial.
Passo 2
Primeiro vamos escrever as equações. Temos que nossas funções de onda são:
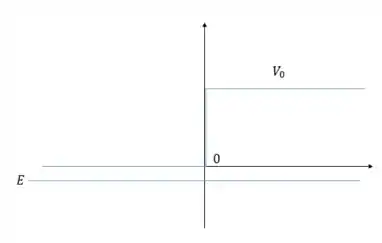
pois após passar a barreira de potencial a onda se extinguira. Se avaliarmos bem, a onda na região I não oscilará, ou seja, terá apenas a componente exponencial decrescente. Sendo assim, nossas equações ficaram:
Aplicando a situação de contorno em , teremos que:
Se aplicarmos, ficamos com:
O que nos dá que . Se analisarmos isso, veremos que não é possível que a função tenha esse valor de energia, pois com não haverá a função de onda na região I, ou seja, não haverá onda, o que não é verdade. Assim mostramos que a energia precisa ser maior que zero.
Resposta
Ei, a resposta está no passo a passo :)