Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 3.Problemas - Ex. 1
No problema do macaco e caçador da seção 3.1, mostre analiticamente que a bala atinge o alvo e calcule em que instante de tempo isso ocorre dada uma altura do galho, distancia entre os objetos e a velocidade inicial da bala.
Passo 1
Nesse exemplo dado, no momento em que o macaco vê o clarão do disparo ele se desprende do galho, mas como a gravidade atua da mesma forma nos 2 corpos independentemente da sua velocidade horizontal, a bala e o macaco sempre estarão na mesma altura, tranquilo? Vamos só escrever isso com umas letrinhas e tá feito.
Passo 2
A bala tem velocidade inicial e uma distância do macaco, ambos inicial numa altura
Vamos calcular a altura da bala para cada instante de tempo Como sua altura depende apenas da componente vertical então o movimento nessa direção é acelerado pela gravidade.
Como a bala não tem velocidade, inicialmente, na vertical:
É um movimento de queda livre na vertical.
Já o macaco tem movimento unicamente vertical, mas ele parte do repouso, então sua velocidade inicial também é nula. Vamos olhar para sua altura
Logo, chegamos a conclusão de que em qualquer instante de tempo, pois só dependem da gravidade local, que é a mesma pros 2 objetos.
Passo 3
Para saber em que instante ocorre a colisão precisamos saber a distância e com que velocidade a bala saiu, certo? Vem comigo!
O movimento horizontal da bala pode ser descrito assim, supondo uma distância entre a bala e o macaco e a posição inicial da bala sendo :
Esse é o tempo necessário para a bala atingir o macaco, a uma distância horizontal e uma altura .
Só que nós temos esse triângulo aqui para a visualização do problema:
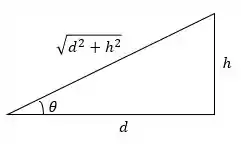
Como pode ser escrito como , temos: