Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.6 - Ex. 39
Um rifle que atira balas a é apontado para um alvo situado a de distância. Se o centro do alvo está na mesma altura do rifle, para que altura acima do alvo o cano do rifle deve ser apontado para que a bala atinja o centro do alvo?
Passo 1
Então galera, o movimento como um todo pode ser dividido em movimento uniforme em relação ao eixo e movimento uniformemente variado em relação ao eixo , pois se trata de um lançamento oblíquo, show? Dêem uma olhada na figura que exemplifica o problema :
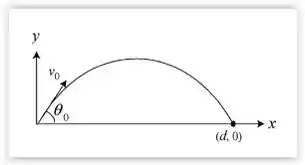
A primeira coisa que devemos fazer, portanto , é calcular a velocidade inicial em função de em relação aos dois eixos:
E:
Além disso, podemos tirar que o deslocamento na horizontal é dado como:
Logo, o tempo que a bala disparada leva para atingir o alvo é:
Passo 2
Em relação ao eixo vertical, por sua vez, temos que:
Para saber o tempo que ela demora para antigir o alvo, temos que saber o tempo que ela demora para chegar em e, como parte da mesma altura, temos que . Além disso, vamos substituir , pois a aceleração aponta para baixo e que achamos ali em cima:
Tal que:
Substituindo que achamos no passo anterior:
Usando a relação , obtemos que:
Portanto, subsituindo os valores:
Obtemos assim que:
Passo 3
Para atingir o centro do alvo, o rifle deve visar um ponto a uma altura acima do alvo tal que:
Ou seja, vamos formar o triângulo retângulo em que os catetos são e . Assim:
Subsituindo os valores: