Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 67

Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve:

a. Redigir um problema realista para o qual esta seja a equação correta.

b. Fazer uma representação pictórica.

c. Solucionar o problema proposto.

1 2 100   k g v 2 2 - 6,67 × 10 - 11   N m 2 / k g 7,36 × 10 22   k g 100   k g 1,74 × 10 6   m = 0 - 6,67 × 10 - 11 N m 2 / k g 7,36 × 10 22 k g 100   k g 3,48 × 10 6   m

Passo 1

Esse é um “exercício” em que devemos criar um enunciado com base na expressão dada. Neste caso, temos a equação:

1 2 100   k g v 2 2 - 6,67 × 10 - 11   N m 2 / k g 7,36 × 10 22   k g 100   k g 1,74 × 10 6   m = 0 - 6,67 × 10 - 11 N m 2 / k g 7,36 × 10 22 k g 100   k g 3,48 × 10 6   m

onde a nossa incógnita é v 2 . Vamos tentar identificar os termos:

  • 100   k g é a massa, m do nosso corpo;

    • Logo, 1 2 100 v 2 2 é a energia cinética final do nosso corpo.

  • 6,67 × 10 - 11   N m 2 / k g é a constante universal da gravitação, G .
  • 7,36 × 10 22 k g será a massa M de um planeta;
  • 1,74 × 10 6   m será a distância final, r 2 , do nosso corpo ao centro do planeta;
  • 3,48 × 10 6   m será a distância inicial, r 1 , do nosso corpo ao centro do planeta.
  • 0 será a energia cinética inicial.

Note que - G m M r 2 = U f (energia potencial final); - G m M r 1 = U i (energia potencial final). Portanto, a equação dada é a conservação da energia mecânica:

K f + U f = K i + U i

onde K f = 1 2 m v 2 2 e K i = 0 .

Passo 2

  1. Dessa forma, podemos montar o seguinte enunciado:

    2. Um corpo de massa m = 100   k g é liberado, a partir do repouso, a uma distância de 3,48 × 10 6   m do centro de um planeta de massa M = 7,36 × 10 22   k g . Qual será a velocidade do corpo quando estiver a uma distância de 1,74 × 10 6   m do centro do planeta?

    Passo 3

  2. Temos o seguinte esquema:

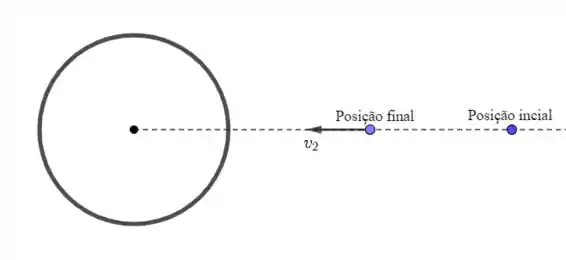
    3. Passo 4

  3. Resolvendo para v 2 , temos:

1 2 100 v 2 2 - 6,67 × 10 - 11 7,36 × 10 22 100 1,74 × 10 6 = - 6,67 × 10 - 11 7,36 × 10 22 100 3,48 × 10 6 v 2 = 1680   m / s

Resposta

A velocidade do corpo será 1680   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espaçonave está viajando ao longo da reta que liga o centro da Terra ao centro da Lua. A que distância da Terra a força gravitacional total que a Terra e a Lua exercem sobre a a nave é zero?
Um satélite de 125k g de massa está em uma órbita circular de raio 7,00.10 6m em torno de um planeta. Se o período é 8050s , qual é a energia mecânica do satélite?
Qual é a variação percentual da aceleração percentual da aceleração da Terra em direção ao Sol quando o alinhamento entre a Terra, o Sol e a Lua muda de um eclipse do Sol (com a Lua entre a Terra e o
Vários planetas (Júpiter, Saturno, Urano) possuem anéis, talvez formados por fragmentos que não chegaram a formar um satélite. Muitas galáxias também contêm estruturas em forma de anéis. Considere um
12.54. Suponha que a órbita da Lua em torno da Terra seja circular. A partir do período orbital de 27,3 dias, calcule a distância da Lua ao centro da Terra. Suponha que o movimento da Lua seja determi