Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve:
a. Redigir um problema realista para o qual esta seja a equação correta.
b. Fazer uma representação pictórica.
c. Solucionar o problema proposto.
Passo 1
Esse é um “exercício” em que devemos criar um enunciado com base na expressão dada. Neste caso, temos a equação:
Vamos tentar identificar alguns termos dessa equação:
- é a constante universal da gravitação, .
- é a massa da Terra. Note que você não precisava saber esse valor “de cara”. Basta você ir nas últimas páginas do livro, que lá tem os dados astronômicos! :)
- . Note que esse valor aparece nos dois lados da equação! Esse valor será a massa, , de nosso satélite!
- é a velocidade, , que o nosso satélite está orbitando a Terra.
- é a distância entre o satélite e o centro da Terra.
Agora, vamos tentar reconhecer as fórmulas. Do lado direito, temos (colocando as letras no lugar dos números!)
Essa fração representa a força gravitacional entre o planeta e o nosso satélite!
Do outro lado, temos
Essa equação fração representa a força centrípeta que o satélite está sujeito!
Portanto, temos que
Assim, podemos pensar em um problema onde um satélite está em órbita ao redor da Terra.
Passo 2
- Podemos pensar no seguinte problema:
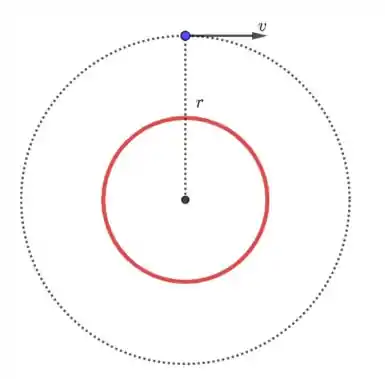
- Temos o seguinte esquema:
- Resolvendo para , temos
Qual deve ser a distância, medida a partir do centro do planeta Terra, que um satélite (massa 1.000 kg) deve ficar para que ele fique em órbita com uma velocidade de 1.997 m/s?
Passo 3
Passo 4
Resposta
Portanto, o satélite deveria estar a .