Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 71

Num ônibus espacial, em uma órbita de 300 km de altitude, precisa-se realizar uma experiência a uma distância considerável da nave. Para tanto, uma carga útil de 100 kg é “baixada” em direção à Terra por uma corda praticamente sem massa com 10 km de comprimento. (Não entraremos em detalhes sobre como isso é feito e vamos simplesmente supor que seja possível.) Após a experiência realizada, a carga útil pode ser trazida de volta para bordo do ônibus. Suponha que quaisquer movimentos iniciais associados com o ato de baixar a carga útil tenham sido neutralizados e que o ônibus e a carga útil estejam voando em condição estacionária um em relação ao outro.

a. Qual é o ângulo da corda em relação a uma linha imaginária traçada pelo centro da Terra e da carga útil? Explique.

b. Qual é a tensão na corda?

Passo 1

A figura abaixo ilustra o que o enunciado diz.

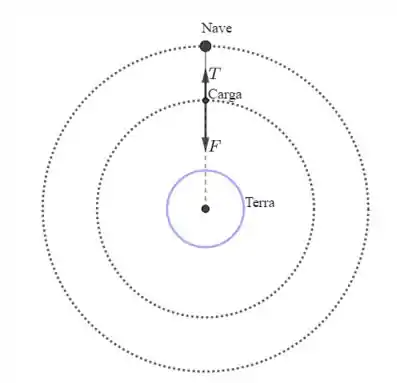
Note que tanto a carga quando a nave, estão movendo em órbitas circulares ao redor da Terra. Poderemos, portanto, usar nosso conhecimento sobre gravitação e movimento circular para resolver a questão!

Passo 2

  1. Foi pedido qual deve ser o ângulo entre a corda e a linha imaginária. Note o seguinte: Se a corda fizesse um ângulo θ ≠ 0 , então a carga faria um movimento circular acelerado, pois haveria uma componente da tração na direção tangencial ao círculo descrito pela carga. Porém, isso não pode ocorrer (já que o movimento da nave é um MCU, desde de que o enunciado diz que o movimento da carga não influencia no movimento da nave). Sendo assim, o ângulo deve ser necessariamente igual a 0°!!

    2. Passo 3

  2. A velocidade angular da nave e da carga deve ser igual (para manter o ângulo da corda igual a 0°).
  • Cálculo do período da nave: a força gravitacional entre a Terra é componente centrípeta:

    • m v 2 R = G m M R 2 ⟹ v = G M R

    Logo,

    ω = v R = G M R 3

  • Cálculo do período da carga: a força resultante é F - T , onde F é a força gravitacional entre a Terra e a carga e T a tração. Suponha que r seja a distância entre a carga e o centro de Terra e que m seja a massa da carga. Logo,

F - T = m v 2 R G m M r 2 - T = m v 2 r G m M r 2 - T = m R ω r 2 G m M r 2 - T = m ω 2 r T = G m M r 2 - m ω 2 r T = G m M r 2 - m G M R 3 r T = G m M 1 r 2 - r R 3 T = G m M r 2 1 - r 3 R 3

Notemos que r = R T e r r a + 290   k m e R = R T e r r a + 300   k m , onde R T e r r a é o raio da Terra, R T e r r a = 6371   k m . Logo,

T = 6,67 × 10 11 100 5,98 × 10 24 6661 × 10 3 2 1 - 6661 × 10 3 3 6671 × 10 3 3 T = 4,04   N

Passo 3

Note que a tração é relativamente pequena: apenas 4,04   N o que justifica a afirmativa de que o movimento da carga praticamente não altera o movimento da nave!

Resposta

A tração vale 4,04   N .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas estrelas idênticas, cada uma com massa M, giram em torno do centro de massa das duas estrelas. Cada órbita é circular e possui raio R, de modo que as duas estrelas estão sempre em lados opostos d
Um módulo de aterrissagem lunar, de 4.000k g , encontra-se em órbita 50k m acima da superfície da Lua. Ele deve passar para uma órbita de 300k m de altitude a fim de se conectar à nave-mãe, que levará
A NASA gostaria de colocar um satélite em órbita em torno da Lua de forma que ele permanecesse numa mesma posição acima da superfície lunar. Qual é a altitude da órbita do satélite?
Um satélite orbitando a Terra encontra-se diretamente acima de um ponto do equador, à meia-noite, a cada dois dias. Porém, não se encontra sobre esse ponto em nenhum outro momento. Qual é o raio da ór
Um ônibus espacial encontra-se em uma órbita circular a 250k m de altitude. Ele deve se transferir para uma órbita circular de 610k m de altitude a fim de chegar no Telescópio Espacial Hubble e fazer