Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve:
a. Redigir um problema realista para o qual esta seja a equação correta.
b. Fazer uma representação pictórica.
c. Solucionar o problema proposto.
Passo 1
Esse é um “exercício” em que devemos criar um enunciado com base na expressão dada. Neste caso, temos o conjunto de equações:
Vamos tentar identificar alguns termos:
- é uma massa elevada! Portanto, vamos pensar que é a massa de um planeta, digamos .
- também é uma massa elevada! Vamos pensar que é a massa de um outro planeta, digamos .
- é a constante universal da gravitação, .
- será a distância inicial, , entre os centros dos planetas.
- será a distância final, , entre os centros dos planetas.
- será a velocidade final de .
- será a velocidade final de
- Os dois no lado direito da segunda equação representa as energias cinéticas iniciais de cada planeta. Logo, .
Assim, a primeira equação será escrita como:
Note que tal equação é simplesmente a conservação do momento!
A segunda equação poderá ser escrita como:
Note que os termos e são as energias cinéticas inicias de e 2, respectivamente. Além disso, é a energia potencial final e é a energia potencial final. Portanto, essa equação representa a conservação da energia!
Passo 2
- Assim, podemos pensar no seguinte enunciado:
- Temos o seguinte esquema:
- Agora, basta resolver as equações:
Dois planetas de massas respectivamente iguais a e estão com os centros separados de , inicialmente em repouso. Devido a atração gravitacional mútua, eles começam a se aproximar. Qual será a velocidade de cada planeta quando a separação entre seus centros for ?
Passo 3
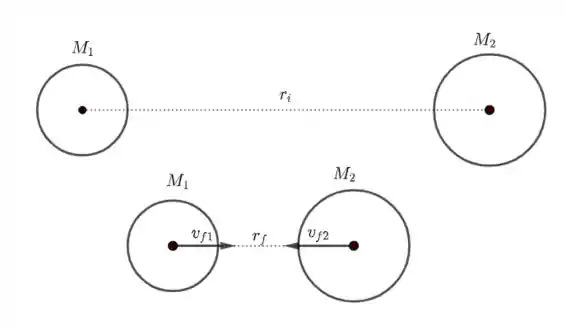
Passo 4
Da primeira equação, tiramos que
Substituindo na segunda, temos que
Assim,
Resposta
Temos e .