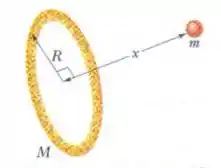
Vários planetas (Júpiter, Saturno, Urano) possuem anéis, talvez formados por fragmentos que não chegaram a formar um satélite. Muitas galáxias também contêm estruturas em forma de anel. Considere um anel fino homogêneo de massa e raio externo . (a) Qual é a atração gravitacional que o anel exerce sobre uma partícula de massa localizada no eixo central, a uma distância do centro? (b) Suponha que a partícula do item (a) seja liberada a partir do repouso. Com que velocidade a partícula passa pelo centro do anel?

Agora vamos considerar um pedaço bem pequeno do anel. Por exemplo, qual é a distância entre o centro da partícula e a ponta da seta que indica o raio na figura?

Pelo teorema de Pitágoras:

E vamos supor que a massa desse “pedacinho” do anel seja , e entre ele e a partícula esteja um pedacinho da energia potencial:

Como a distância entre qualquer ponto do anel e a partícula é o mesmo, todas as grandezas na fórmula acima são constantes, então a energia potencial total é:

Obs.: Outra forma de ver isso é integrar ambos os lados da equação. A integral de será e a integral de será , já que todos os outros parâmetros são constantes.

Agora vamos lembrar de outra fórmula importante. Quando estamos em um único eixo:

Derivando:

Como só estamos interessados no módulo da força:

Pronto, essa é a resposta da letra (a).

Se a partícula de massa é liberada a partir do repouso, queremos saber com que velocidade ela chega ao centro do anel.

Como a força sobre esse massa depende da distância , vamos ter que a aceleração não é constante, assim vamos ter que fazer essa questão por conservação de energia mecânica!

A energia mecânica inicial será

Lembrando que ela foi liberada do repouso, então a energia cinética é nula.

Ao passar pelo centro do anel a energia mecânica será

Atenção, que no centro do anel a energia potencial não é nula, hein!

Fazendo a conservação de energia mecânica