Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.Problemas Adicionais - Ex. 73

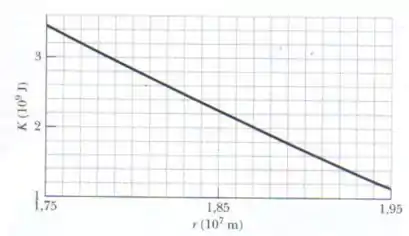
A figura abaixo é um gráfico da energia cinética K de um asteroide que cai em linha reta em direção ao centro da Terra, em função da distância r entre o asteroide e o centro da Terra. (a) Qual é a massa (aproximada) do asteroide (b) Qual é a velocidade do asteroide para r = 1,945   .   10 7   m ?

Passo 1

Vamos utilizar a lei da conservação de energia para resolver essa questão:

K 1 + U 1 = K 2 + U 2

K 1 - G M m r 1 = K 2 - G M m r 2

Agora vamos tomar alguns pontos no gráfico para usar essa equação para resolver a questão.

Passo 2

Escolhendo dois pontos quaisquer no gráfico:

r 1 , K 1 = ( 1,77.10 7 m   ,   3,2.10 9   J )

r 2 , K 2 = ( 1,89.10 7 m   ,   1,8.10 9   J )

Substituindo isso na lei de conservação:

3,2.10 9 - G M m 1,77.10 7 = 1,8.10 9 - G M m 1,89.10 7

1,4.10 9 = G M m 1 1,77.10 7 - 1 1,89.10 7

Agora substituindo as constantes:

1,4.10 9 = m 6,67.10 - 11 5,98.10 24 3,58.10 - 9

m = 1,4.10 9 6,67.10 - 11 5,98.10 24 3,58.10 - 9 = 1,0.10 3   k g

Passo 3

Vamos usar a fórmula para energia cinética:

K = m v 2 2

Olhando o gráfico, podemos ver que quando r = 1,945   .   10 7   m   , K   ≈ 1,2.10 9   J , ou seja:

1,2.10 9 = 10 3 v 2 2

v = 2,4.10 9 10 3 = 1,5   .   10 3   m / s

Pronto!

Resposta

(a) m =   1,0.10 3   k g

(b) v = 1,5   .   10 3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um satélite de massa de 200k g é colocado em órbita da Terra a uma altura de 200k m acima da superfície. (a) Assumindo uma órbita circular, quanto tempo o satélite leva para completar uma órbita? (b)
54 . Astrônomos detectam um meteoroide distante movendo-se ao longo de uma linha reta que, se prolongada, passaria a uma distância de 3 R T do centro da Terra, em que R T é o raio dessa. Qual é a velo
46 . Muitas pessoas acreditam que a resistência do ar, agindo sobre um corpo em movimento, sempre irá torná-lo mais lento. Ela pode, no entanto, ser responsável por torná-lo mais rápido. Considere um
45 . Uma nave espacial está se aproximando de Marte depois de uma longa viagem a partir da Terra. Sua velocidade é tal que está viajando ao longo de uma trajetória parabólica sob a influência da força
60 . A nave espacial do Observatório Solar e Heliosférico (Soho) tem uma órbita especial, localizada entre a Terra e o Sol ao longo da linha que os interliga, e está sempre perto o suficiente da Terra