Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 103
Você assite seu amigo jogando hóquei. Durante o jogo, ele atinge o disco de tal forma que, ao chegar no seu ponto mais alto, o disco passa de raspão por cima do muro de acrílico de 2,80 m de altura que cerca o campo, distante 12,0 m de jogador. Encontre (a) a componente vertical da velocidade inicial, (b) o tempo para atingir o muro e (c) a componente horizontal da velocidade inicial, a rapidez inicial e o ângulo de lançamento. (Ignore a resistência do ar.)
Passo 1
Oi galera, tudo bem? É muito importante tentar visualizar direitinho toda a situação apresentada no problema. Pra te ajudar, trouxe aqui um desenho que esquematiza tudo certinho.
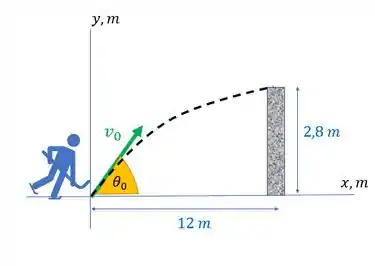
O jogador bate no disco com uma velocidade inicial inclinada em relação a horizontal. Por isso ela vai subir.
O disco atinge a altura máxima justamente quando passa de raspão no muro, por isso a altura do muro é a altura máxima da trajetória... guarda essa informação. Temos também que o muro está a uma distância de 12 m do jogador.
Agora vamos ver quais equações podemos usar pra resolver nosso problema. O movimento vertical e o movimento horizontal são independentes. Então a gente analisa cada um deles com equações diferentes.
O movimento da horizontal (em x) não possui aceleração, ou seja, ela é zero. Então o movimento é uniforme. Por isso para resolver o problema usaremos:
Onde
Na vertical, como a aceleração é a gravidade, o movimento é acelerado. Por isso podemos usar as equações:
Onde . E tem o sinal de menos porque consideramos o positivo para cima.
Vamos usar essas equações para resolver nosso problema, belezinha?
Passo 2
a) A questão nos pede a componente vertical da velocidade INICIAL .
Uma informação bem importante é que a velocidade da componente vertical no momento mais alto da trajetória é sempre zero pois é o momento em que ela troca de sentido. Então temos que no ponto de maior altura
Já que não temos nenhuma informação sobre o tempo podemos usar a equação de torriceli pra descobrir essa velocidade. Vamos usar os dados do instante mais alto.
Uma coisa para não confundir. Como estamos vendo a componente vertical da velocidade, usamos , o deslocamento máximo vertical do disco que é a altura do muro.
Passo 3
b) A questão também pede o tempo para atingir o muro.
Como já temos a velocidade inicial então é só substituir na equação da velocidade para achar o tempo.
Passo 4
c) A questão também nos pediu para encontrarmos a componente horizontal da velocidade inicial, a rapidez inicial e o ângulo de lançamento.
Para isso podemos começar usando a equação do espaço horizontal para achar a velocidade horizontal inicial:
Por que? Porque agora temos o tempo que leva para o disco atingir altura máxima, que é o tempo achado no itm anterior. E sabemos que a posição do disco na altura máxima é a distância dele do jogador, então é .
E a posição inicial no nosso referencial é zero mesmo. Substituindo nossos dados:
Passo 5
Sabendo os valores de e , podemos fazer a razão entre eles para achar uma relação entre eles e , que é o ângulo de lançamento:
Substituindo nossos dados e isolando :
Resolvendo temos que
Com esses dados fica fácil de achar a rapidez inicial do movimento. A rapidez inicial do movimento é o módulo da velocidade inicial do movimento. Então tudo que a gente precisa fazer é achar o valor de . A gente viu lá no passo 1 que
Isolando quem a gente quer e substituindo o que temos: