Um projétil é lançado com velocidade formando um ângulo com a horizontal. O ponto de lançamento está situado a uma altura acima do solo.

1. Desprezando a resistência do ar, mostre que a distância horizontal percorrida pelo projétil antes de ele atingir o solo é dada por:

Verifique que, se o ponto de lançamento estivesse situado no mesmo nível do solo, isto é, , essa expressão se reduziria ao alcance horizontal encontrado no Exemplo .

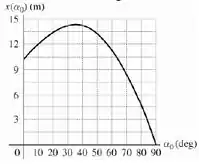
b) Para o caso e , faça um gráfico de em função do ângulo de lançamento para valores de de a . Seu gráfico deve mostrar que é igual à zero para , mas é diferente de zero para ; explique a razão disso.

c) Vimos no Exemplo que, quando o projétil atinge o solo no mesmo nível em que ele é lançado, o alcance horizontal é máximo para . Para o caso desenhado no item o ângulo de lançamento para o alcance horizontal máximo é igual a, maior que ou menor que ?

(Este problema fornece um resultado geral para o lançamento de um projétil lançado de um ponto mais elevado do que o ponto onde ele atinge o solo.).

Começando pela letra a), vamos fazer um esqueminha do lançamento aqui pra ficar mais claro tá?

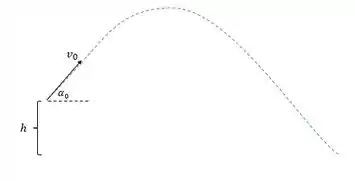
Para acharmos a distância horizontal percorrida, que eu vou chamar de , teremos que analisar separadamente os movimentos vertical e horizontal do projétil, beleza?

Bora lá!

Vamos começar pelo movimento horizontal. Como em um lançamento obliquo o movimento horizontal é um movimento retilíneo uniforme, temos que:

Isso porque não há aceleração na horizontal.

Considerando que , temos:

Note que a equação dada na questão não está em função do tempo, então vamos utilizar o movimento vertical para acharmos o tempo

O movimento vertical é um movimento uniformemente acelerado, sendo a aceleração igual a gravidade, então temos que:

Sabendo que:

Temos:

Podemos reorganizar:

Resolvendo pela fórmula de Báskara:

Perceba que:

E como o tempo é um valor positivo, temos que:

Tranquilo até aqui?

Agora só temos que substituir o valor de na expressão para a distância percorrida e chegamos na fórmula desejada:

Show?

Vamos só verifica rapidinho o que a questão pede para verificarmos.

Fazendo nessa expressão:

Teremos:

Juntando os termos semelhantes:

Mas pela identidade trigonométrica daí temos a relação do alcance que já conhecemos:

Estamos quase lá!

Até que enfim chegamos na letra b!!

Para e a expressão para fica:

x por :

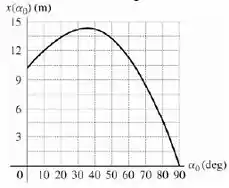
Quando temos temos que o projétil é lançado diretamente na direção vertical, ou seja, pra cima ou para baixo. Assim o movimento na horizontal é nulo, por isso para .

Já quando , o vetor velocidade é puramente horizontal e por isso é diferente de zero, e se não temos uma altura inicial, o objeto vai se mover apenas na direção horizontal.

Bacana, não é?

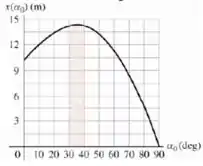
E por último, a letra c

Analisando o gráfico vemos que o máximo de é atingido em um ângulo menor do que .

E aí! o que achou? Responde Aí!