Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.2 - Ex. 5
Um trem com uma velocidade constante de se move na direção leste por , depois em uma direção que faz um ângulo de a leste com a direção norte por e, finalmente, na direção oeste por mais . Quais são
o módulo e
o ângulo da velocidade média do trem durante a viagem?
Passo 1
Desenhando o trajeto percorrido pelo trem nós teremos algo como:
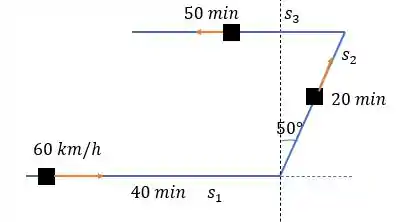
Na letra queremos calcular o módulo da velocidade desse trem mas primeiro temos que calcular o módulo da distância percorrido por ela, uma vez que a velocidade é constante e tem um vetor proporcional a ela. E para começar a fazer essa questão vamos calcular o vetor distância de cada trecho.
Dessa forma no primeiro trecho representa uma distância de:
Onde é o vetor da distância.
Temos que converter o tempo de deslocamento para horas caso queiramos encontrar a distância vetorial de cada trecho. Então:
Encontrando a distância vetorial do segundo trecho e do terceiro trecho nós teremos:
E a distância vetorial de :
Então a distância vetorial total do trajeto será:
O módulo da distância será então de:
Passo 2
Só que queremos na letra o módulo da velocidade do trem e para isso nós temos que fazer:
Onde o tempo percorrido pelo trem em horas será de:
Logo o módulo da velocidade será de:
Passo 3
Como o vetor da velocidade é proporcional ao vetor posição equivalente então podemos afirmar que:
Então o vetor velocidade terá uma ângulo de:
E como o tempo é constante e é de ele não faz diferença para a angulação do vetor velocidade resultante, já que a velocidade é constante pra todos os trechos.