Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 97

Quatro planetas idênticos formam um quadrado, como mostrado na Figura 11-20. Se a massa de cada planeta é M e o lado do quadrado tem comprimento a , qual deve ser a rapidez de cada planeta, se eles devem permanecer em órbita em torno de seu centro comum, sob influencia de suas atrações mútuas?

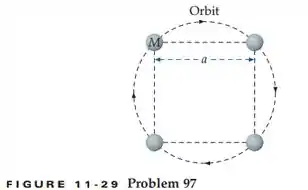
Passo 1

Para resolver essa quetão, basta olharmos para um planeta, pois nosso sistema é simétrico. Fazendo umas ilustração para facilitar nossa vida, temos:

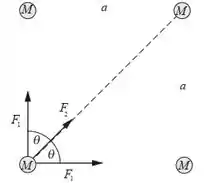
Repare que devido a simetria, o nosso centro de massa será o centro desse quadrado.

Passo 2

Como o CM é o centro do quadrado, vamos decompor as forças nessa direção para acharmos a resultante centrípeta.

F c = F 2 + 2 F 1 cos ⁡ θ

Como temos um quadrado, θ = 45 ° .

F c = F 2 + 2 F 1 ⋅ 2 2 = F 2 + F 1 2

Agora vamos achar F 1 e F 2 .

F 1 = G M M a 2 = G M 2 a 2

Para F 2 , a distância será a diagonal.

F 2 = G M M ( a 2 ) 2 = G M 2 2 a 2

Passo 3

Juntando o que encontramos, temos:

F c = F 2 + F 1 2

Logo,

F c = G M 2 2 a 2 + G M 2 a 2 2 = G M 2 a 2 1 2 + 2

Como a resultante é centrípeta:

F c = M v 2 r

O raio será metade da diagonal.

F c = M v 2 a 2 2

Portanto,

M v 2 a 2 2 = G M 2 a 2 1 2 + 2

Isolando v , temos:

v = G M a ⋅ 2 4 + 1 ≅ 1,16 G M a

Resposta

v = 1,16 G M a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.5. Uma nave espacial interplanetária passa em um ponto do espaço no qual a força de atração gravitacional da Terra sobre a nave cancela a força de atração gravitacional do Sol sobre a nave. a) Qual
12.8. Uma massa pontual de 8,0 kg e outra massa pontual de 15,0 kg são mantidas fixas a 50,0 cm de distância. Uma partícula de massa m é solta de um ponto entre as duas massas a 20,0 cm da massa de 8,
12.1. Calcule a razão da força de atração gravitacional entre o Sol e a Lua e a força entre a Terra e a Lua. Suponha que a distância da Lua ao Sol seja aproximadamente a mesma distância da Terra ao So
12.7. Um homem adulto típico possui massa igual a 70 kg. Qual é a força que a Lua cheia exerce sobre esse homem quando ele está diretamente sobre ele a uma distância de 378000 km? B) Compare essa forç
12.6. a) Qual é o módulo, a direção e o sentido da força gravitacional resultante exercida pelas outras esferas sobre a esfera uniforme de 0,100 kg indicada na Figura 12.31? Os centros das três esfera