Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 82

Uma rede de difração com d = 1,50   μ m é iluminada por uma luz cujo comprimento de onda é 600   n m com vários ângulos de incidência. Faça um gráfico (no intervalo de 0 a 90 ° ) do ângulo entre a direção do máximo de primeira ordem e a direção de incidência em função do ângulo de incidência.

Passo 1

Vamos supôr que um raio de luz difratado na nossa rede produz um máximo de primeira ordem no ângulo θ .

Se o ângulo de incidência desse raio era ψ , sabemos que vale a seguinte relação:

d sen ⁡ ψ + sen ⁡ θ = m λ

De forma que o ângulo θ é:

sen ⁡ θ = m λ d - sen ⁡ ψ

E pelo enunciado temos m = 1 , λ = 600   n m = 0,600   μ m e d = 1,50   μ m , então:

θ = arcsen ⁡ 0,6 1,5 - sen ⁡ ψ

Passo 2

Queremos fazer um gráfico do deslocamento angular total do raio incidente (desde quando ele chega até ser refratado), em função do ângulo de incidência.

Vamos fazer um desenho para entender melhor essa relação:

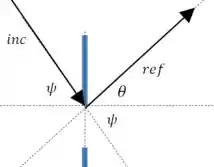
O deslocamento que quremos calcular é a soma daqueles dois ângulos:

α = θ + ψ

Então:

α ψ = arcsen ⁡ 0,6 1,5 - sen ⁡ ψ + ψ

Agora é só fazer o gráfico dessa função quando ψ varia entre 0 ° e 90 ° , ou 0 até π / 2 (em radianos):

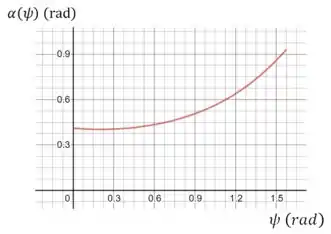
Resposta

A função é α ψ = arcsen ⁡ 0,6 1,5 - sen ⁡ ψ + ψ .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura mostra um gráfico de intensidade em função da posição angular θ para a difração de um feixe de raios X por um cristal. A escala do eixo horizontal é definida por θ s = 2,00 ° . O feixe contém
Na figura, um feixe de raios X com comprimentos de onda entre 95,0p m e 140p m faz um ângulo θ = 45 ° com uma família de planos refletores com um espaçamento d = 275p m . Entre os máximos de intensida
Na figura, a reflexão de primeira ordem nos planos indicados acontece quando um feixe de raios X com um compirmento de onda de 0,260n m faz um ângulo de 63,8 ° com a face superior do cristal. Qual é o
Na figura, um feixe de raios X com um comprimento de onda de 0,125n m incide em um cirstal de NaCl fazendo um ângulo de θ = 45,0 ° com a face superior do cristal e com uma famíia de planos refletores.
Considere uma estrutra cristalina bidimensional quadrada, como, por exemplo, um dos lados da estrutura que aparece na figura. A maior distância interplanar dos planos refletores é a 0 , a dimensão da