Uma rede de difração tem ranhuras por milímetro e é iluminada por luz branca com incidência normal. Uma figura de difração é observada em uma tela, a da rede. Se um furo quadrado com de lado é aberto na tela, com o lado interno a do máximo central e paralelo a esse máximo, determine (a) o menor e (b) o maior comprimento de onda da luz que passa pelo furo.
Passo 1
Vamos começar fazendo um desenho para representar a situação:
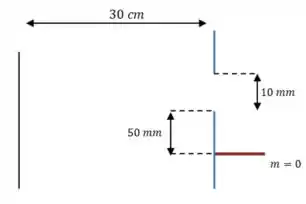
Podemos usar esse desenho para determinar a posição angular da borda do furo quadrado:
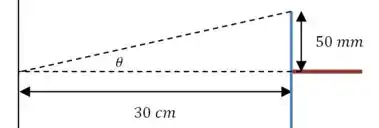
E além disso, sabendo que temos ranhuras a cada milimetro da rede de difração, podemos calcular o valor da distância entre as ranhuras:
Passo 2
(a) Agora que conhecemos esses valores, vamos ver como o nosso padrão de interferência se comporta na borda do furo:
Como estamos tratando de luz branca (que é uma combinação de vários comprimentos de onda na faixa visível), temos .
Isso quer dizer que o único resultado inteiro possível para é (para ter , por exemplo, precisaríamos de , o que é “proibido” aqui).
E se :
E esse é o menor comprimento de onda da luz que passa pelo furo. Para encontrar o maior, temos que olhar para a outra extremidade.
Passo 3
(b) Vamos calcular o ângulo para a extremidade externa do furo:
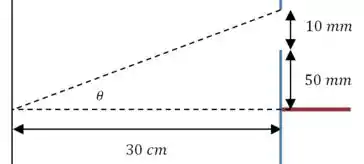
E fazendo a mesma conta de antes, obtemos o seguinte:
E pela mesma lógica de antes, temos como o maior comprimento de onda que passa pelo furo.
Resposta
(a) O menor comprimento de onda que passa pelo furo é .
(b) O maior comprimento de onda que passa pelo furo é .