Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 5.Exercícios e Problemas - Ex. 10
Referindo-se ao Exercício 5.9, para um valor fixo de , a que ângulo de lançamento o projétil atinge a distância d máxima?
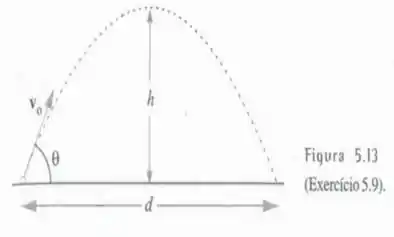
Passo 1
Meus amigos e minhas amigas, essa questão trata-se de um problema muito legal.
A questão nos pede o ângulo no qual d atinge a distância máxima.
Sabemos que o tempo total (subida e descida) é dado por:
Agora, vamos aplicar essa fórmula a equação do deslocamento horizontal:
Teremos:
Como estudantes inteligentes que somos, conhecemos a seguinte igualdade trigonométrica:
Portanto:
Como queremos para termos uma distância máxima, vamos derivar d em função de e igualar a zero!
Simplificando ambos os lados da equação por :
Sabemos que o ângulo que possui cosseno igual a zero é o de .
Logo:
Resposta
Exercícios de Livros Relacionados
Uma moeda de 5,0g encontra-se a 15c m do centro de uma plataforma giratória. A moeda tem coeficientes de atrito estático e cinético com a superfície da plataforma que valem, respectivamente, μ e = 0,8
Demonstre as Equações 8.4 para a aceleração de um projétil sujeito a uma força de arraste.
Uma bola de borracha é solta e cai sobre uma rampa inclinada em 20 ° , como mostra a FIGURA PD4.82. O ricocheteio da bola obedece à “lei da reflexão”, ou seja, a bola deixa a superfície de impacto for
Você é convidado a realizar uma consulta médica em um hospital de pesquisa da cidade onde um grupo de doutores está pesquisando o bombardeio de tumores cancerosos por íons de alta energia. Os íons são
21. Alice fixa um modelo pequeno de foguete a um disco de hóquei no gelo de 400g . O foguete gera 8,0N de empuxo. Alice orienta o disco de modo que o foguete aponte seu nariz no sentido positivo do ei