Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 33
Uma moeda de encontra-se a do centro de uma plataforma giratória. A moeda tem coeficientes de atrito estático e cinético com a superfície da plataforma que valem, respectivamente, e . A plataforma acelera muito lentamente até
. A moeda escorregará para fora?
Passo 1
Olá, tudo bem?
Vamos anotar primeiro todos os dados (nas unidades do SI) que o problema nos trás:
E queremos saber se a moeda vai escorregar para fora. Isso significa que o problema pergunta se a velocidade angular que a plataforma chega é suficiente para contrabalançar a força de atrito da moeda com a superfície. Lembrando que essa velocidade angular está relacionada com a força centrípeta, certo?
E quanto às forças existentes no problema? Bom, sempre temos a gravidade, apontando verticalmente para baixo. No nosso caso, como a moeda está sobre uma plataforma, a gravidade está contrabalançada pela força normal. Lembrando que aqui não temos movimento na vertical, apenas na horizontal, em cima dessa plataforma.
E temos também, ao longo da direção radial, a força centrípeta. No nosso caso ela deve ser igual à força de atrito estático para que a moeda não escorregue certo?
O problema nos dá os dois coeficientes de atrito: estático e cinético, mas você não deve se confundir! O atrito estático é aquela força de resistência ao movimento quando o objeto está em repouso. Ela é maior que o atrito cinético e impede que o objeto seja posto em movimento. Ela varia e tem seu valor máximo quando , onde é o módulo da força normal. Quando a força aplicada supera esse valor , o objeto é posto em movimento, e aí que entra a força de atrito cinético. Ela é responsável por se opor ao movimento enquanto o objeto se move. Ela possui um valor fixo de e estará presente enquanto o movimento acontecer.
Tranquilo?
Pra visualizar melhor, vamos fazer um esboço da situação:
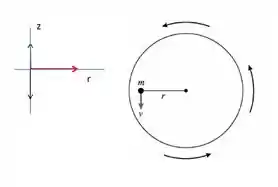
No lado direito temos uma vista de cima do movimento. A moeda está em movimento de rotação em cima de uma plataforma giratória. No desenho do lado esquerdo, está um diagrama de forças. No eixo vertical as duas flechas representam os vetores das forças normal e gravitacional. Como não temos movimento nesse sentido, esses vetores possuem mesmo módulos e direções opostas, sendo assim:
E em vermelho está representada a força centrípeta, que nesse caso, deve ser igual à força de atrito estático:
Passo 2
Agora vou usar essas duas expressões e encontrar uma para a velocidade:
Por fim:
E substituindo os valores de e que anotamos lá no começo do passo
Podemos achar o valor da velocidade:
Passo 3
Agora com a velocidade linear, podemos achar a velocidade angular:
Essa é a velocidade angular máxima que a moeda pode suportar antes de começar a escorregar. Mas o problema nos diz que a plataforma acelera até . Então para fazer a comparação, precisamos transformar o valor que encontramos em . Para isso é simples: basta multiplicar o valor em por =D
Saca só:
A plataforma acelera até , então a moeda não vai escorregar para fora da plataforma =)
Beleza?
Espero ter ajudado!
Vamos pra próxima?