Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 7.Problemas - Ex. 4
Relacione a direção de desvio do elétron de recuo no efeito Compton (Seç. 7.4) com as frequências e dos fótons incidente e espalhado e o ângulo e de espalhamento.
Passo 1
Vamos entendero que está acontecendo:
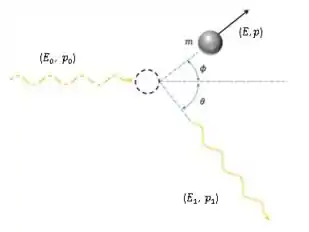
O fóton colide com um elétron em repouso, que adquire uma energia cinética. E o fóton é espalhado.
Utilizando a equação de conservação do momento linear:
Primeiro, vamos olhar para a direção vertical:
Então
Show!
Olhando agora na direção horizontal:
Dividindo uma equação pela outra teremos:
Mas,
Esse é a frequência, também podemos escrever . Mas aqui ele pede em termos de . Então...
Onde é a frequência dos fótons incidentes e é a frequência dos fótons espalhados.
Substituindo;
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Mostre que se um fóton de energia E for espalhado por um elétron livre em repouso, a energia cinética máxima do elétron espalhado será K m a x = E 2 E + m c 2 / 2
Um fóton sofre espalhamento Compton por parte de um eletron livre estacionário. O ângulo de espalhamento é 90 ° em relação à direção inicial e o comprimento de onda inicial é 3,00 ⋅ 10 - 12m . Qual a
Determine (a) o deslocamento de Compton Δ λ ; (b) o deslocamento de Compton relativo Δ λ / λ ; (c) a variação da energia Δ E de um fóton pertencente a um feixe luminoso com um comprimento de onda λ =
Calcule a variação percentual da energia do fóton em uma colisão como a da Fig. 38-5 para ϕ = 90 ° e uma radiação (a) na faixa de micro-ondas, com λ = 3,0c m ; (b) na faixa da luz visível, com λ = 500
Um feixe de raios X com um comprimento de onda de 0,0100n m , no sentido positivo so eixo x , incide em um alvo que contém elétrons quase livres. Para o espalhamento de Compton a 180 ° de um fóton por