Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 13
O vetor quantidade de movimento angular de spin de uma roda que gira em torno de seu eixo é paralelo ao eixo e aponta para o leste. Para levar este vetor a apontar para o sul, em que sentido deve ser exercida uma forças sobre a extremidade leste do eixo? (a) para cima, (b) para baixo, (c) para o norte, (d) para o sul, (e) para o leste.
Passo 1
Qual a relação entre o torque e o momento angular?
Ou seja, para mudar o vetor , é preciso que haja um torque . Podemos escrever a forma “integral” dessa expressão da seguinte forma:
Quando o vetor começa a mudar sua direção, o vetor aponta para o sul:
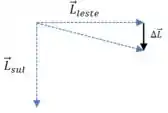
Então o vetor também aponta para o sul, já que a nossa equação ali de cima nos diz que é paralelo a .
Passo 2
Em que direção devemos exercer uma força para que ela gere um torque que aponta para o sul?
Como a força será exercida na extremidade leste da roda, o vetor posição da força apontará para a direita (paralela a ), e então:
Pela regra da mão direita, só existe uma direção de que satisfaz essa relação:
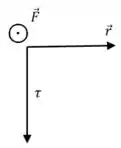
É o caso em que está saindo do plano da página. Ou seja, em que aponta para cima.
Resposta
Letra (a).