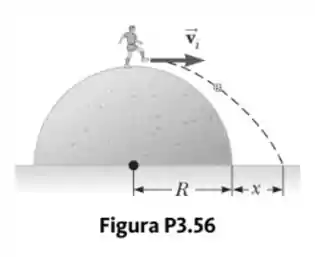
Uma pessoa em pé sobre uma pedra esférica de raio chuta uma bola (inicialmente em repouso no topo da pedra) para lhe dar velocidade horizontal  , como mostrado na Figura P3.56.

1. Qual deve ser a velocidade inicial mínima da bola se ela não deve tocar a pedra após ser chutada?
2. Com essa velocidade inicial, a que distância da sua base a bola atinge o chão?

Agora, a equação do círculo é dado por:

Como a bola não bate na pedra em nenhum ponto, o y do projétil é sempre maior que y do círculo. Consequentemente, nós devemos ter:

Agora, a equação acima é verdadeira para qualquer valor arbitrário de x, mesmo que x = 0. Portanto, nós devemos ter:

Consequentemente, a velocidade mínima deve ser , se a bola nunca tocar na pedra.

Letra b:

O tempo que a bola leva para ler o chão é:

Então,

Consequentemente, a distância da base da pedra é