Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 92
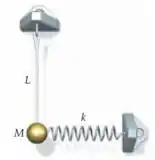
A figura mostra um pêndulo de comprimento com uma bolinha de massa . A bolinha é presa a uma mola de constante de força , como mostrado. Quando a bolinha está diretamente abaixo do suporte do pêndulo, a mola está frouxa. (a) Deduza uma expressão para o período de oscilação do sistema para pequenas amplitudes de vibração. (b) Suponha que e tal que, na ausência da mola, o período é . Qual é a constante de força , se o período de oscilação do sistema é ?
Passo 1
a) Ele quer uma expressão para o período de oscilação desse pêndulo que tem influência da mola.
Vamos começar com um diagrama da situação quando o pêndulo está deslocado por um ângulo em relação à vertical:
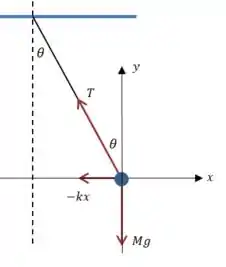
Vamos supor (como aproximação), que o pêndulo (a bolinha azul) permanece em uma mesma linha horizontal já que temos pequenas amplitudes de vibração ( máximo é bem pequeno), então as forças em devem estar em equilíbrio, e teremos apenas uma aceleração na horizontal.
Pelo equilíbrio, teremos
Pela primeira equação, temos que:
Substituindo isso na segunda:
Passo 2
Vamos mexer um pouco nessa equação que encontramos.
Podemos relacionar a aceleração com o ângulo , lembrando lá de movimento circular.
A aceleração angular da bolinha azul é
Podemos achar a aceleração na direção da trajetória multiplicando isso pelo raio da trajetória, que é aproximadamente :
Assim, substituindo na equação
Passo 3
Lembra que em bem pequeno, então a coordenada com o mesmo ângulo pode ser aproximada por um arco. A dimensão de um arco é ângulo vezes raio, então podemos escrever:
(não colocamos o sinal de menos aqui porque já o consideramos na hora de escrever a força na equação de equilíbrio)
E considerando pequenos ângulos, podemos usar a seguinte aproximação:
Agora vamos substituir tudo isso na equação do passo anterior
Isso é uma equação diferencial porque relaciona uma grandeza e sua derivada.
Passo 4
Essa é a equação diferencial tá igualzinha à equação do oscilador harmônico, que nós já conhecemos bem. Ela tem essa cara:
A solução geral segue a seguinte forma:
Onde é a frequência angular. Comparando essa forma geral com a nossa equação, concluímos que:
E como a relação entre o período e a frequência angular é , o período de pequenas oscilações do nossos sistema é:
Como o enunciado pediu!
Passo 5
b) Na ausência da mola temos , de forma que a equação final do item anterior fica
Se nesse caso o período é , então:
Passo 6
E então, no caso em que o período é e a massa é , e há presença da mola, teremos:
Repara que substituímos ali, beleza?
Podemos resolver essa equação para encontrar a constante de força :
Resposta
(a) .
(b) .