Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 120

A figura mostra um cilindro oco de 1,80 m de comprimento e 0,80 k g de massa, com raio igual a 0,20 m . O cilindro pode girar em torno de um eixo vertical que passa perpendicularmente pelo seu centro. Dois objetos estão dentro do cilindro. Cada objeto tem 0,20 k g de massa e está preso a uma mola de constante de força k e comprimento igual a 0,40 m , quando frouxa. As paredes internas do cilindro são sem atrito. (a) Determine o valor da constante de força, se os objetos estão localizados a 0,80 m do centro do cilindro, quando este gira a 24   r a d / s . (b) Qual é o trabalho necessário para levar o sistema do repouso até esta rapidez angular de 24   r a d / s ?

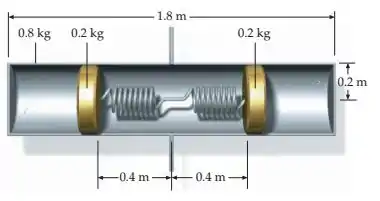
Passo 1

  1. Sacou o que vai acontecer aqui? Quando o sistema começar a girar, as massas vão se deslocar para fora, fazendo aparecer uma força centrípeta, que será a resultante da força da mola.

    2. F r a d i a l = k Δ x = m r ω 2

    Mas r = x + Δ x :

    k = m x + Δ x ω 2 Δ x

    Substituindo valores:

    k = 0.20 0.80 24 2 0.40

    k = 230 N / m

    Passo 2

  2. O trabalho feito sobre o sistema vai ser o responsável por criar a rotação e a deformação das molas. Então, pela conservação de energia:

W = K r o t + U m o l a

W = I ω 2 2 + k Δ x 2 2

O momento de inércia vai ser a soma do momento de inércia da mola e do cilindro.

I = I c i l i n d r o + 2 I d i s c o

O momento de inércia da casca cilíndrica é:

I c i l i n d r o = M r 2 2 + M L 2 12

Para as massas, que são discos finos, o eixo não passa no lugar que estamos acostumados, então vamos ter que usar o teoremas dos eixos paralelos. Da figura a gente pode ver que a distância ao centro de massa é x .

I d i s c o = m r 2 4 + m x 2

Então o momento de inércia vai ser:

I = M r 2 2 + M L 2 12 + 2 m r 2 4 + m x 2

Temos esses valores: M = 0.80 k g , m = 0.20 k g , R = r = 0.2 m , L = 1.80 m e x = 0.8 m .

É só substituir agora! Fazendo isso, vamos obter:

I = 0.492   N ⋅ m 2

Agora é só voltar na equação da energia e substituir!

W = 0.492 × 24 2 2 + 230 × 0.40 2 2

W = 0.16 k J

Resposta

  1. k = 230 N / m
  2. W = 0.16 k J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema da figura, análogo a um regulador centrífugo, o anel A, de massa desprezível, pode deslizar ao longo do eixo vertical. Inicialmente, as duas bolas iguais de massa m = 200 g estão a uma dist
Existem relatos de guepardos correndo à velocidade impressionante de 114k m / h , feitos por observadores que dirigiam ao lado desses animais. Imagine o que é tentar medir a velocidade de um guepardo
Uma partícula de 4,0k g se move em um plano x y . No instante em que a posição e a velocidade da partícula são r → = 2,0i ^ + 4,0j ^ m e v → = - 4,0j ^m / s , a força que age sobre a partícula é F → =
108- Um disco de vinil gira a 33 1/3 rev/min no prato de um toca-discos. (a) Qual é a velocidade angular do disco em radianos por segundo? Qual é a velocidade linear em um ponto do disco (b) a 15 cm e
15 . Uma patinadora começa um giro com os braços esticados para os lados. Ela se equilibra na ponta de um patim para girar sem atrito. Em seguida, puxa seus braços de modo que o momento de inércia dim