Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 12.5 - Ex. 27

O sistema da figura ao lado está em equilíbrio. Um bloco de concreto com uma massa de 225   k g está pendurado na extremidade de uma longarina com uma massa de 45,0   k g . Para os ângulos ϕ   =   30,0   º e θ   =   45,0   º , determine a) a tensão T do cabo e as componentes b) horizontal e c) vertical que a dobradiça exerce sobre a longarina

Passo 1

(a) Vamos chamar de λ o ângulo entre a longarina e o cabo, podemos fazer o DCL assim:

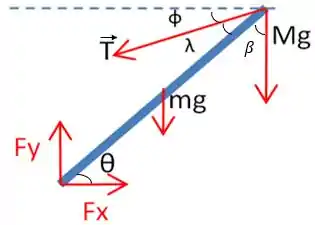
M g : peso do bloco.

m g : peso da longarina.

F x e F y são as componentes da força que a dobradiça exerce na longarina.

T → : tensão do cabo.

Repare que subimos com ϕ , pela relação de trigonometria mesmo (por curiosidade: são ângulos alternos internos).

Vamos chamar também de β o ângulo formado entre a longarina e a vertical. Podemos perceber que β = 90 ° - θ = 45 ° . Com isso, temos que ϕ + λ + β = 90 ° . Nesse caso, com ϕ = 30 ° e β = 45 ° , vamos achar que λ = 15 ° .

Passo 2

Do equilíbrio de torques com relação à dobradiça (ou seja, F x e F y não entram na conta, pois elas estão sobre o eixo, logo não exercem torque em relação a ele), considerando L como sendo o comprimento da longarina, temos:

T ∙ L s e n λ = M g L s e n β + m g L 2 s e n β

Substituindo os ângulos:

T L s e n 15 ° = M g L s e n 45 ° + m g L 2 s e n 45 °

Então, podemos simplificar o L :

T s e n 15 ° = M g s e n 45 ° + m g 1 2 s e n 45 °

Colocando g   s e n ⁡ ( 45 ° ) em evidência e isolando T :

T = g s e n 45 ° M + m 2 s e n 15 °

Substituindo os valores:

T = 225 + 45 2 9,81   .   s e n ⁡ ( 45 ° ) s e n ⁡ ( 15 ° ) = 6 , 63 ∙ 10 3   N

Passo 3

(b)Considerando o equilíbrio horizontal do sistema, temos:

F x = T cos ⁡ ϕ

F x = 6 , 63 ∙ 10 3 N ∙ cos ⁡ 30 °

F x ≅ 5,74 ∙ 10 3 N

Passo 4

(c) Finalmente, o equilíbrio das componentes verticais nos fornece:

F y = T s e n ϕ + M g + m g

F y = 6 , 63 ∙ 10 3 ∙ s e n 30 ° + 225 ∙ 9,81 + 45 ∙ 9,81

F y = 5 , 96 ∙ 10 3 N

Resposta

(a)

6 , 63 ∙ 10 3   N

(b)

5,74 ∙ 10 3 N

(c)

5 , 96 ∙ 10 3 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de aço de 1,50m de comprimento e 1,00m m de diametro está ligado a um fio de alumínio de dimensões identicas, compondo um fio de 3,00m de comprimento. Determine a variação de comprimento que re
A corda mi de um violino, de aço, está sob uma tração de 53,0N . O diametro da corda é 0,200m m e o comprimento quando tracionada, é 35,0c m . Determine (a) o comprimento desta corda, quando não traci
Durante um experimento de ciência dos materiais, sobre o modulo de Young da borracha, a professora fornece à sua equipe uma tira de borracha de seção reta retangular. Ela lhes diz para primeiro medir
Uma tora homogênea , de 100 k g de massa, 4,0m de comprimento e 12c m de raio, é mantida em uma posição inclinada como mostrado na Figura 12-44. O coeficiente de atrito estático entre a tora e a super
Duas massas, M 1 e M 2 , estão suspensas por fios que têm comprimento iguais quando frouxos. O fio que suporta M 1 é de alumínio e tem 0,70m m de diâmetro, e o que suporta M 2 é de aço e tem 0,50m m d