Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.6 - Ex. 61
Suponha que, na Eq. 15-45, a amplitude é dada por:
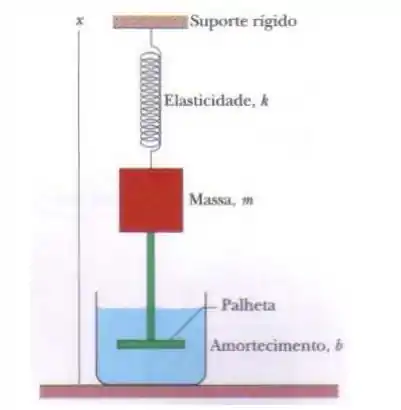
onde é a amplitude (constante) da força alternada externa exercida sobre a mola pelo suporte rígido da Fig 15-14. Qual é, na ressonância, (a) a amplitude do movimento e (b) a amplitude da velocidade do bloco?
Passo 1
Belezoca galerinha, pra acharmos a amplitude de oscilação na ressonância, basta impormos que:
Na equação da amplitude em função da frequência dada pelo enunciado. Logo:
Passo 2
Pra acharmos a amplitude da velocidade do bloco, basta a gente saber que:
Então, na ressonância, teremos:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
Neste problema, você deve usar o resultado do problema 105 para deduzir a Equação 14-51. Na ressonância, o denominador da fração entre colchetes no problema 105(e) é b 2 ω 0 2 e P m é d i a é tem seu
Neste problema, você deve deduzir a expressão para a potência média desenvolvida por uma força de excitação sobre um oscilador forçado.Mostre que a potência instantânea desenvolvida pela força de exci
Determine a frequência de ressonância para cada um dos três sistemas mostrados na figura:
Um corpo de 2,00k g oscila preso a uma mola que tem uma constante de força igual a 400N / m . A constante de amortecimento linear vale b = 2,00k g / s . O sistema é exictado por uma força senoidal de
Um oscilador linearmente amortecido perde 2,00 por cento de sua energia em cada ciclo. (a) Qual é o seu fator Q ? (b) Se sua frequência de ressonância é 300H z , qual é a largura da curva de ressonânc