Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 57

Um tanque cilíndrico com um grande diâmetro é preenchido com água até uma profundidade D = 0,30 m . um furo de seção transversal de área A = 6,5   c m ² no fundo do tanque permite a drenagem da água. (a) Qual é a vazão com que a água é drenada, em metros cúbicos por segundo? (b) A que distância abaixo do fundo do tanque a área de seção transversal da corrente se iguala á metade da área do furo?

Passo 1

(a) A presença do furo, assim como na questão 56, tira o fluido de sua condição de repouso. Como o escoamento nesse caso é incompressível, podemos utilizar novamente a equação de Bernoulli para descrever como a pressão varia com a altura e a velocidade do fluido.

Segundo a equação de Bernoulli:

p + 1 2 ρ × v ² + ρ × g × y = c o n s t a n t e

Nesse caso, tomamos o fundo do recipiente como o referencial de altura y .

Passo 2

Agora, vamos aplicar a equação de Bernoulli em pontos localizados na superfície do fluido (onde p = p 2 e y = h 2 ) e no furo (onde p = p 1 , y = h 1 e v = v 1 ), notando que a velocidade na superfície do fluido é desconsiderada por que o diâmetro do tubo é muito grande (ver exercício 56 para relembrar o por quê disso).

Assim, temos :

p 2 + ρ × g × D = p 1 + 1 2 ρ × v 1 2  

Como a superfície está em contato com a atmosfera assim como o furo: p 2 = p 1 = p a t m o s f é r i c a . Desenvolvendo a expressão anterior com base nisso, temos:

ρ × g × D = 1 2 ρ × v 1 2

Logo:

v 1 = 2 × g × D = 2 × ( 9,8 m s 2 ) × 0,3   m = 2,42   m / s

E a vazão é dada por

Q = v A = 2,42 × 6,5 × 10 - 4 = 1,57 × 10 - 3   m 3 / s

Lembrando que 6,5   c m 2 = 6,5 10 - 2 m 2 = 6,5 × 10 - 4   m 2 !

Passo 3

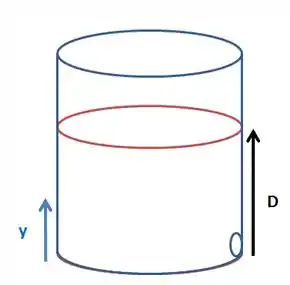
(b) Aqui, vamos utilizar a equação da continuidade. Considerando um ponto a uma altura y ' abaixo do fundo do fundo do recipiente como indicado na figura, onde a área do jato d’áua e sua velocidade são iguais a A ' e v ' , temos:

A 1 × v 1 = A ' × v '

v ' = A 1 A ' × v 1 = 2 × v 1 = 4,84 m s

Passo 4

Aplicando agora a equação de Bernoulli entre um ponto no furo e na região onde y = y ' , temos:

p a t m o s f é r i c a + 1 2 ρ × v 1 2 = p a t m o s f é r i c a + ρ × g × y ' + ρ × v ' 2 2

Logo:

y ' = 1 2 g × v 1 2 - v ' 2 = 1 2 × 9,8 m s 2 ×   2,42 m s 2 - 4,84 m s 2 ≅ - 0,90   m

Resposta

  1. 1,57 × 10 - 3 m 3 / s
  2. 0,90   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura 13-39, H é a profundidade do líquido e h é a distância da superfície do líquido ao tubo inserido no lado do tanque. (a) Encontre a distância x em que a água atinge o chão depois de sair do t
Derive a equação de Bernoulli da maneira com mais generalidade do que é feito no texto, ou seja, permita que o fluido mude de altitude durante seu movimento. Usando o teorema de trabalho-energia, most
Um barril grande de altura H e área de seção transversal A 1 é preenchido com cerveja de raiz. O topo está aberto à atmosfera. Há uma abertura de torneira da área A 2 que é muito menor do que A 1 na p
No Exemplo 13-11, o fluido é acelerado ao entrar em uma parte estreita do tubo. Identifique as forças que atuam sobre o fluido na entrada da região estreita, responsáveis pela aceleração.
Um tubo horizontal se estreita de um diâmetro de 10 cm, na localização A, para um diâmetro de 5 cm, na localização B. Para um fluido incompressível e não-viscoso que escoa sem turbulência de A para B,