Um tanque cilíndrico longo e fechado contém um gás diatômico que é mantido a uma temperatura uniforme, que pode ser variada. Quando você mede a velocidade do som v no gás em função da temperatura T do gás, obtém estes resultados:
(a) Explique como você pode representar esses resultados em um gráfico, de modo que ele se ajuste a uma linha reta. Construa esse gráfico e verifique se os pontos plotados estão próximos de uma linha reta. (b) Como o gás é diatômico, 'Y = 1,40. Use a inclinação da reta no item (a) para calcular M, a massa molecular do gás. Expresse M em gramas/mol. Que tipo de gás se encontra no tanque?
Passo 1
Fala galera, bora lá! Para este exercício, utilizaremos da variação da velocidade do som em um gás para encontrar os valores pedidos.
(a) A equação da velocidade do som para um gás, em função da temperatura é dada por:
Onde a temperatura está apresentada em Kelvins e a constante do gás vale
Passo 2
É possível montar uma tabela com os valores da raiz quadrada da temperatura, comparando com a velocidade do som, obtendo:
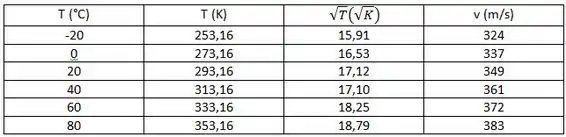
Passo 3
Agora se montarmos um gráfico com os valores da velocidade do som em função da raíz quadrada da temperatura, obtemos:
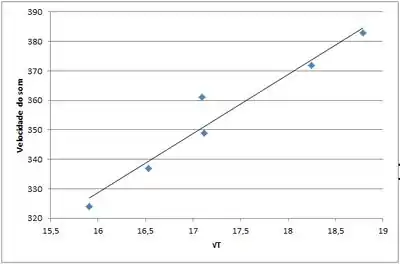
Sendo possível então perceber, que o comportamento deste gráfico é linear. Portanto, se utilizarmos a raiz quadrada da temperatura, em kelvins, para gerar o gráfico, o comportamento do mesmo será linear.
Passo 4
(b) O coeficiente angular desta reta pode ser encontrado pela razão entre a variação de dois pontos, dado pela equação:
Passo 5
A equação desta reta é dada por:
Com isso, é possível perceber que o coeficiente angular vale:
Passo 6
Então a massa molar pode ser encontrada por.
Como , podemos substituir todos os valores para encontrar.
Resposta
- Se utilizarmos a raiz quadrada da temperatura, em kelvins, para gerar o gráfico, o comportamento do mesmo será linear.
- A massa molar deste gás vale , valor próximo ao da massa molar do alumínio.