Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 64
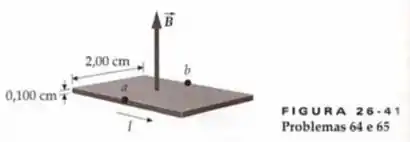
Uma tira metálica de de largura e de espessura, conduz uma corrente de em uma região com um campo magnético uniforme de , como mostrado na Figura 26-41. A tensão Hall medida é de . (a) Calcule a rapidez de arraste dos elétrons livre na tira. (b) Determine a densidade de número de elétrons livres na tira. (c) Qual dos pontos, ou , está em um potencial mais elevado? Explique sua resposta.
Passo 1
Esse é um problema em que vamos discutir sobre o efeito Hall. Vamos adotar um sistema de coordenadas:
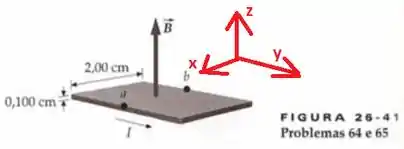
O produto é dado por
Desta forma, as cargas positivas serão desviadas para o ponto e a negativa para o ponto . Isso significa que o campo elétrico vai apontar de para , de modo que
Isso já responde o item (c)!
Passo 2
No item (a) ele pede a velocidade dos portadores de carga. Pelo que você deve ter visto sobre efeito Hall, a força elétrica deve anular o força magnética :
A tensão se relaciona com o campo elétrico por
Assim,
Substituindo os valores:
Passo 3
Para o item (b) vamos usar a relação apresentada no capítulo
Assim,
Sabemos que , , e :
Portanto,