Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas adicionais - Ex. 84

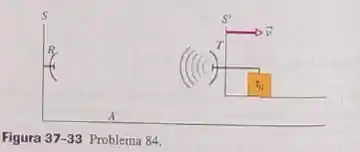
Um transmissor de radar T está em repouso em um referencial S ´ que se move para a direita com velocidade v em relação ao referencial S(Fig.37-33). Um contador mecânico ( que pode ser considerado um relógio) do referencial S´, com um período τ o ( no referencial S ´ ), faz com que o transmissor T emita pulsos de radar, que se propagam com a velocidade da luz e são recebidos por R, um receptor do referencial S. (a) Qual é o período τ do contador do ponto de vista do observador A, que está em repouso no referencial S? (b) Mostre que, no receptor R, o intervalo de tempo entre os pulsos recebidos não é τ em τ o , mas

τ R = τ o c + v c - v

(c) Explique por que o receptor R e o observador A, que estão em repouso no mesmo referencial, medem um período diferente para o transmissor T. (Sugestão: um relógio em um pulso de radar não são a mesma coisa.)

Passo 1

Como a fonte está se movendo nós teremos efeitos relativísticos de dilatação temporal que são dados pela transformada de Lorentz:

  1. Segundo a equação 37-7 nós teremos que o período observado por A será:

    2. τ = γ τ o = 1 1 - v c 2 τ o

    Passo 2

  2. O período observado por R será o inverso da frequência emitida pela fonte, Logo:

    3. τ R = 1 f r mas devido a efeitos relativísticos e a fonte está se movendo contra R nós teremos que:

    f r = f o 1 - v c 2 1 + v c 2   , logo τ R = 1 / ( f o 1 - v c 2 1 + v c 2 )

    τ R = τ o . 1 + v c 2 1 - v c 2

    τ R = τ o c 2 - v 2 c 2 ( c 2 + v 2 ) 1 c 2      

    τ R = τ o c 2 - v 2 c 2 + v 2 = τ o c + v c - v

     

    Passo 3

  3. O efeito Doppler envolve dois diferentes fenômenos: a dilatação do tempo quando a fonte está em movimento e a variação do intervalo dentre os picos acontece quando os sinais periódicos emitidos por uma fonte em movimento são captados por um receptor que está parado com relação a fonte. Para podermos medir o efeito de dilatação do tempo nós precisamos usar medidas que comparem as leituras de um relógio em movimento com as de dois relógios do observador parado.

Resposta

a ) 1 1 - v c 2 τ o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 37-27 mostra um gráfico da intensidade em função do comprimento de onda da luz emitida pela galáxia NCG 7319, que está a aproximadamente 3 ⋅ 10 8a n o s - l u z da Terra. O pico mais intenso
Uma lâmpada de sódio está se movendo em círculos em um plano horizontal, com uma velocidade constante de 0,1c, enquanto emite luz com um comprimento de onda próprio λ 0 = 589n m . Um detector situado
26. Mostre que, se uma fonte de ondas eletromagnéticas se afasta de nós com velocidade igual a 0,600 c , a frequência que medimos é igual à metade da frequência mediada no sistema no qual a fonte está
Reescreva a Equação 37.25 para encontrar a velocidade relativa u entre a fonte eletromagnética e um observador em termos da razão entre a fraquencia observada e a frequência da luz da fonte. Que veloc
Medida de elocidade com radar. Um instrutor de beisebol usa um radar para medir a velocidade de uma bola de beisebol. Sse dispositivo envia ondas eletromagnéticas com frequência f 0 e a seguir mede o