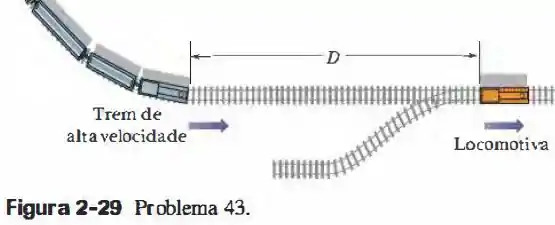
Quando um trem de passageiros de alta velocidade que se move a faz uma curva, o maquinista leva um susto ao ver que uma locomotiva entrou indevidamente nos trilhos através de um desvio e se encontra a uma distância à frente (Fig. ). A locomotiva está se movendo a . O maquinista do trem de alta velocidade imediatamente aciona os freios. (a) Qual deve ser o valor mínimo do módulo da desaceleração (suposta constante) para que a colisão não ocorra? (b) Suponha que o maquinista está em quando, no instante , avista a locomotiva. Desenhe as curvas de da locomotiva e do trem de alta velocidade para os casos em que a colisão é evitada por pouco e a colisão ocorre por pouco.

Então primeiro, vamos usar a equação de Torricelli para o trem:

Onde o deslocamento do trem vai ser igual a distância mais o deslocamento da locomotiva :

Podemos também estabelecer uma relação entre a aceleração, tempo e velocidade para o trem: , de modo que a equação se torna:

E lembrando do produto notável , podemos abrir a relação da velocidade como:

Logo:

E agora colocando em evidência, vemos que:

Belezoca, então para que a aceleração seja mínima é preciso que a velocidade do trem quando chegar até a locomotiva seja igual à da locomotiva . Agora é só substituirmos isso na equação e dar uma arrumadinha, saca só:

Então quer dizer que descobrimos a fórmula que define a aceleração nesse caso, agora vamos passar as velocidades para metros por segundo e substituir na equação.

Logo a aceleração será:

Então o módulo da aceleração vai ser: :