Considere um vetor no sentido positivo do eixo , um vetor no sentido positivo do eixo e um escalar . Qual é a orientação de se é (a) positivo e (b) negativo? Qual é o mnódulo de (c) e (d) ? Qual é a orientação (e) de e (f) ? (g) Qual é o módulo de ? (h) Qual é o módulo de ? Qual é(i) a amplitude e (j) a orientação de se é positivo?
Passo 1
(a) Por enquanto nós só sabemos que aponta no sentido positivo de e aponta no sentido positivo de :
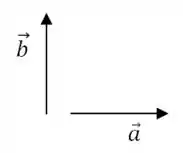
Quando dividimos o vetor por um escalar , a sua direção sempre continua igual. Mas a sua magnitude e o seu sentido podem mudar.
No caso em que é positivo, o sentido de continua o mesmo (apontando para cima), mas a sua magnitude pode aumentar (se ), continuar igual () ou diminuir ).
Ou seja, aponta no sentido positivo do eixo .
Passo 2
(b) No caso em que é negativo, o sentido do vetor vai se inverter: ele vai apontar na vertical para baixo. E assim como antes, sua magnitude pode aumentar ou diminuir.
Passo 3
(c) Agora vamos fazer o produto escalar de e .
Como os dois vetores são perpendiculares, o seu produto escalar é sempre nulo:
Se não lembrar disso, você pode usar a fórmula para o produto escalar:
Onde é o módulo do vetor , e assim por diante, e é o ângulo formado pelos dois vetores. No caso em que :
Passo 4
(d) Agora queremos calcular o módulo do seguinte produto escalar:
Como vimos lá em cima, dividir um vetor por um escalar nunca altera a direção do vetor.
Isso quer dizer que os vetores vão continuar sendo perpendiculares, e então o produto escalar vai continuar sendo nulo.
Passo 5
(e) Para descobrir a orientação do produto vetorial, temos que usar a regra da mão direita.
Ao contrário do produto escalar, o produto vetorial produz um vetor. E a regra da mão direita é quem dá a orientação desse vetor. Essa regra é muito usada na física. Você só precisa seguir alguns passos.
Aponte o seu indicador na direção e sentido do vetor , e o seu dedo médio na direção e sentido do vetor . Agora estenda o seu polegar.
A direção para onde o seu polegar aponta é a direção do produto vetorial.
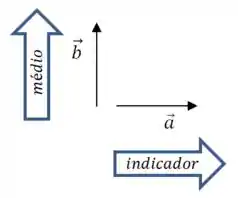
Agora seu polegar deveria estar apontando para fora da página, em uma direção perpendicular aos dois vetores.
Passo 6
(f) Agora vamos mudar um pouco as coisas:
Quando trocamos a ordem de um produto vetorial ( ao invés de ) a única diferença no resultado é o sinal.
Ou seja, se antes o resultado era um vetor perpendicular ao plano da página e saindo dela, agora o resultado é um vetor entrando nela.
Outra forma de ver isso é usando a regra da mão direita mais uma vez:
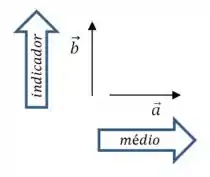
Passo 7
(g) Agora queremos calcular o módulo de . Vamos lembrar da fórmula para o módulo de um produto vetorial:
Onde é o ângulo formado pelos dois vetores. Nesse caso, , então:
Passo 8
(h) E o que acontece com o módulo quando trocamos a ordem do produto vetorial?
O ângulo continua sendo :
Como , o módulo continua igual.
Passo 9
(i) Queremos calcular outro módulo de um produto vetorial. Vamos usar a mesma fórmula de antes:
O módulo do vetor é simplesmente o módulo de dividido pelo escalar . Além disso, já que a divisão por escalar não muda a direção de um vetor, o ângulo continua sendo .
Então:
Passo 10
(j) Agora queremos saber a orientação desse produto vetorial:
Já vimos que a divisão por escalar não altera a direção do vetor. E quanto o escalar é positivo, essa divisão também não altera o sentido.
Ou seja, esse produto vetorial terá a mesma orienação que o produto : estará saindo do plano da página.
Resposta
(a) Sentido positivo do eixo .
(b) Sentido negativo do eixo .
(c) Zero.
(d) Zero.
(e) O vetor é perpendicular ao plano da página, saindo dela.
(f) O vetor é perpendicular ao plano da página, entrando nela.
(g) O módulo do produto vetorial é .
(h) O módulo do produto vetorial é .
(i) A amplitude é .
(j) A orientação é perpendicular ao plano da página, saindo dela.