Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 29.Exercícios e Problemas - Ex. 52
Três elétrons formam um triângulo eqüilátero com 1.0 nm de lado. Um próton encontra-se no centro do triângulo. Qual é a energia potencial desse grupo de cargas?
Passo 1
Fala galera, tudo tranquilo? Temos um triângulo equilátero (3 lados iguais) e queremos saber o valor da energia potencial do conjunto de cargas. Os dados que temos em mãos são os lados, um próton e três elétrons:
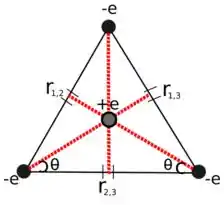
O seguimento liga a carga 1 (carga no topo) até a carga 2 (carga do lado esquerdo), o seguimento liga a carga 1 até a carga 3 (carga do lado direito),
o seguimento como já devem ter percebido, conecta a carga 2 da esquerda até a carga 3 na direita. Como se trata de um triângulo equilátero, já podemos fazer a seguinte igualdade: .
Devemos fazer uma pequena relação com o ângulo para que possamos encontrar a distância até o próton no centro, vamos chamar de “d”.
Devemos levar em conta os ângulos internos do triângulo. Logo .
Passo 2
Sabendo disso agora podemos encontrar “d”:
. Como “d” tem a mesma medida para o próton no centro. Então, todas as outras medidas dos elétrons até o próton no centro, são iguais! A partir disso, basta substituirmos os valores na equação para a energia potencial .
Primeiramente temos os potenciais para os elétrons em cada vértice:
Agora com relação a carga no centro. As medidas dos elétrons com respeito ao próton no centro (vamos chamar de carga 4), assim como o potencial delas são iguais, assim:
Agora fazemos a soma de todas as contribuições