Três resistores, com resistencias de , e , são ligados em paralelo e uma bateria de 28,0 V, que possui resistencia interna desprezivel. Calcule (a) a resistencia equivalente da combinação; (b) a corrente atraves de cada resistor; (c) a corrente tital através da bateria; (d) a voltagem através de cada resistor; (e) a energia dissipada em cada resistor. (f) Qual dos dois resistores dissipa mais energia, aquele que possui a maior resistencia ou o de menor resistencia? Explique por quê.
Passo 1
A equação
fornece a resistência equivalente dos três resistores em paralelo. Para resistores em paralelo, as tensões são as mesmas e as correntes se somam.
Passo 2
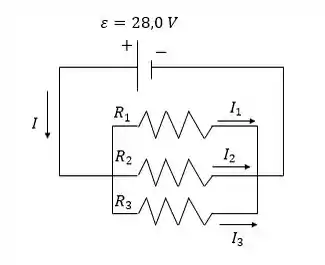
- O circuito é esboçado a seguir:
- Para resistores em paralelo, a tensão é a mesma em cada um e igual à tensão aplicada;
- As correntes através dos resistores são adicionadas para fornecer a corrente através da bateria:
- Como mostrado na parte (b), a tensão em cada resistor é de .
- P odemos usar qualquer uma das três expressões para :
- Podemos perceber que o resistor que dissipa mais energia é o menor resistor, porque como a tensão em cima de cada resistor é igual, a maior corrente circula pelo menor resistor. Elevando a pontência.
Assim, calculando em pararelo:
Passo 3
Então,
E
Passo 4
Passo 5
Como alternativa, podemos usar a resistência equivalente , como mostrado na Figura:
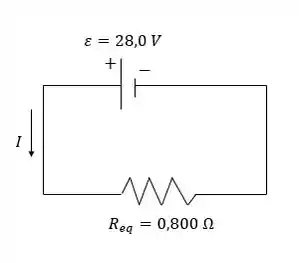
O que se verifica.
Passo 6
Passo 7
Todos eles dão os mesmos resultados, se mantivermos números significativos o suficiente em cálculos intermediários.
Usando :
E
Passo 8
Resposta
- ; ; .
- ; ;
- O menor resistor dissipa a maior potência e energia.