Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 14

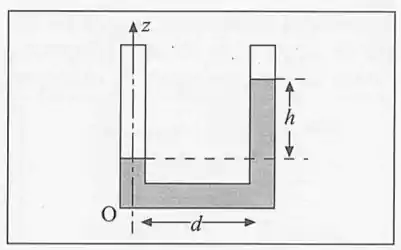
14. Um tubo em U contendo um líquido gira em torno do eixo O z ( F i g .   P . 9 ) , com velocidade angular de 10   r a d / s . A distância d entre os dois ramos do tubo é de 30   c m , e ambos são abertos na parte superior. Calcule a diferença de altura h entre os níveis atingidos pelo líquido nos dois ramos do tubo.

Passo 1

Bora lá pra mais um probleminha sobre fluidos.

Xiii rapaz!! Você deve estar se perguntando como raios é que vamos resolver esse problema, afinal de contas, o tubo está girando em torno do eixo O z . Deve ser dificílimo esse problema.

Mas é ai que você se engana. Essa questão é bem mais simples do que se imagina. O sistema em questão é similar àquele discutido na seçao 1.4 do livro, do líquido em rotação. É possível encontrar uma expressão para a superfície livre utilizando o mesmo procedimento... Por isso, tudo que temos de fazer é utilizar a fórmula abaixo, advinda do livro:

z = ω 2 2 g ⋅ r 2

Esse r é o nosso raio de giro. Como sabemos que a distância d entre os dois ramos do tubo é de 30   c m , então o nosso raio de giro é de 30   c m . Basta então, substituir os outros valores na fórmula:

z = ( 10   r a d / s ) 2 2 ⋅ ( 9,81   m / s 2 ) ⋅ ( 0,30   m ) 2

z ≈ 0,46   m

Viu! Foi mais fácil do que parece. A nossa diferença de altura é de 0,46   m .

Resposta

z ≈ 0,46   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque em forma de L mostrado na Figura está cheio d’água e é aberto na parte de cima. Se d = 5,0m , qual é a força exercida pela água: (a) Na face A e (b) Na face B ?
O tanque em forma de L mostrado na Figura está cheio d’água e é aberto na parte de cima. Se d = 5,0m , qual é a força exercida pela água: (a) Na face A e (b) Na face B ?
Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura
Um tubo em forma de U , aberto nas duas extremidades, contém mercúrio. Quando 11,2c m de água são despejados no lado direito do tubo, de quanto o mercúrio sobe no lado esquerdo em relação ao nível ini
A figura mostra um tubo em forma de U modificado: o lado direito é mais curto que o esquerdo. A extremidade do lado direito está d = 10,0c m acima da bancada do laboratório. O raio do tubo é 1,50c m .