Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.3 - Ex. 18
Atração de uma montanha. Uma grande montanha praticamente não a afeta a direção “vertical” indicada por uma linha de prumo. Suponha que a montanha possa ser modelada por uma esfera de e massa específica . Suponha também que uma linha de prumo de 0,50 m de comprimento seja pendurada a uma distância do centro da esfera e que a esfera atraia horizontalmente o peso da linha de prumo. Qual será o deslocamento do peso da linha de prumo em direção a à esfera?
Passo 1
Primeiramente, é necessário entender a física do problema. O esquema abaixo ajuda a entender o que o problema está pedindo.
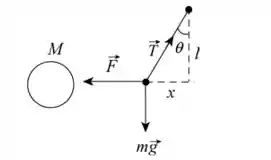
Queremos calcular o deslocamento x. Pra isso, um diagrama de corpo livre resolve o problema. Somando então as forças nas direções horizontal, a gente tem:
Onde, é a força de atração da esfera:
E vertical:
Igualamos as forças resultantes à , pois após a esfera atrair a linha, o sistema entra em equilíbrio.
Daqui, tiramos que:
Passo 2
Pra gente achar a massa da montanha é mole. A gente tem o volume dela e a massa específica. Então, só multiplicar um pelo outro, já que:
Onde é o volume de uma esfera:
Passo 3
Beleza! Combinando agora as duas equações de , a gente já consegue achar x, porque:
E, igualando as duas equações de :
Simplificando :
Passando o para o outro lado:
Passo 4
Como vimos que:
Podemos, agora, substituir o valor da tangente:
Lembrando que queremos isso tudo a uma distância de , ok? Então, substituindo os valores que temos:
Show! Um deslocamento bem pequeniniho, não é mesmo?
Resposta
O deslocamento é de