Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 95

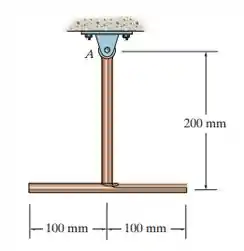
Os elementos finos possuem massa de 4   k g / m . Determine o momento de inércia do conjunto em relação a um eixo perpendicular à página e que passa pelo ponto A .

Passo 1

Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.

Este problema nos pede para determinarmos o momento de inercia em relação ao eixo x conjunto em termos da massa. Sabemos que a massa de cada segmento é dada por:

m i = ( 4   k g / m ) ( 0.2   m ) = 0.8   k g

O momento de inércia de massa de cada segmento do conjunto em torno de um eixo através de seu centro de massa pode ser determinado usando a seguinte relação:

I G i = 1 12 m i l i 2

Assim, o momento de inercia em torno de A vai ser:

I A = ∑ I G i + m i d i 2

Passo 2

Agora, vamos esboçar um esquema para determinarmos as distâncias para os centros de massa, temos:

Com isso, podemos determinar o momento de inercia de massa em torno de A deste conjunto. Como temos 2 barras, nossa relação fica assim:

I A = ∑ I G i + m i d i 2 I A = 1 12 0,8 0,2 2 + 0,8 0,1 2 + 1 12 0,8 0,2 2 + 0,8 0 , 2 2 I A = 0,0453   k g ∙ m

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

I A = 0,0453   k g ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Use a Equação (9.20) para calcular o momento de inércia de uma barra delgada de massa M e comprimento L em relação a um eixo perpendicular à barra e passando pela sua extremidade.
Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Uma placa metálica fina de massa M tem forma retangular com lados a e b . Use o teorema dos eixos paralelos para determinar seu momento de inércia em relação a um eixo perpendicular ao plano da placa