Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 64
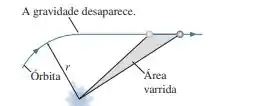
Um planeta está em órbita de uma estrela quando, sem nenhuma razão aparente, a gravidade da estrela desaparece repentinamente. Como ilustra a FIGURA P13.64, o planeta obedece à primeira lei de Newton e passa a se afastar ao longo de uma linha reta. A segunda lei de Kepler ainda é obedecida, ou seja, áreas iguais são varridas em tempos iguais enquanto o planeta se distancia?
Passo 1
O que sabemos sobre a primeira lei de Newton? Sabemos que, na ausência de forças, um corpo irá ou permanecer em repouso, ou irá percorrer uma trajetória retilínea com velocidade de módulo constante (MRU).
No caso do nosso problema, o planeta já estava se movimentando. Logo, quando desaparece a gravidade, ele passará a percorrer uma trajetória reta com velocidade de módulo constante.
A 2° Lei de Kepler, diz basicamente que:
O vetor posição do planeta varrerá áreas iguais em intervalos de tempos iguais!
(lembre-se que vetor posição é o vetor que liga a estrela até o planeta)
À primeira vista, pode parecer que a 2° Lei de Kepler não será mais válida... afinal, ela foi demonstrada utilizando o fato de a força gravitacional ser uma força central (de modo que o momento angular do planeta é constante durante todo o movimento); porém, vamos demonstrar que a 2° lei de Kepler permanecerá válida!!!
Passo 2
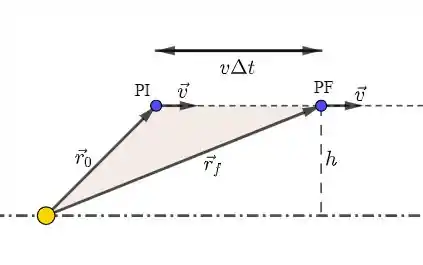
Veja o esquema abaixo, onde:
- O ponto amarelo representa a estrela;
- O ponto azul representa o planeta;
- PI um ponto onde o planeta estava em um tempo ;
- PF é um ponto onde o planeta estava em um tempo .
- é a “altura” da órbita do planeta.
- é a velocidade do planeta (que é constante, conforme vimos acima);
- e são, respectivamente, os vetores posição inicial e final do planeta;
Sendo constante, a distância, , entre PI e PF poderá ser calculada como:
Portanto, a área do triângulo formado pelos vetores posição (região pintada na figura) é:
Assim, temos que
Assim... segue que é uma constante... assim, em intervalos de tempos iguais o planeta irá percorrer áreas iguais! Ou seja, a 2° Lei de Kepler permanecerá válida.
Passo 3
Apenas como aprofundamento, lembre-se da Equação 13.28:
Para o caso da figura, temos:
Portanto, temos
em concordância com a Equação 13.28!!! Porém, isso realmente deveria ocorrer. O fato de a força gravitacional ser central, implica que o torque realizado por ela é nulo! Quando a força gravitacional desaparece, logicamente também não poderá haver nenhum torque... ou seja, saímos de uma situação sem nenhum torque para uma situação também sem nenhum torque. Logo, nada deve mudar na 2° Lei de Kepler.
Resposta
A 2° Lei de Kepler continuará válida!