Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.10 - Ex. 53b
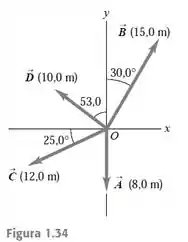
Para os vetores , e indicados na Figura 1.34, ache os produtos escalares b) .
Passo 1
Faala ae, beleza?? Bora lá!
O problema quer que a gente calcule o produto escalar entre os vetores e , ou seja, ele quer:
Sabemos que a o produto escalar resulta em um número, e é dado por:
Dessa forma, nós vamos precisar dos módulos dos vetores e do ângulo entre eles, certo?
Veja só! 😉
Passo 2
Beleza, para achar o módulo desses vetores, podemos olhar para a imagem, que diz os módulos de todos os vetores. Assim, vemos que:
E:
Além disso, podemos achar o ângulo entre e também! Vamos desenhar só os dois para ficar mais simples de ver o ângulo:
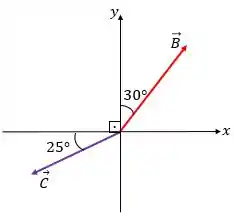
Dessa forma, podemos ver que o ângulo entre esses dois vetores é dado por:
Beleza! Agora, temos tudo o que precisamos para achar o produto escalar entre eles.
Passo 3
Voltando com a nossa fórmula do produto escalar:
Agora, vamos substituir os valores:
Prontinho! Só isso! Entendeu tudo? Responde Aí! 👀
