Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.6 - Ex. 58
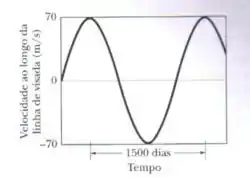
Às vezes, a presença de um planeta invisível associado à estrela distante pode ser deduzida a partir da observação do movimento da estrela. Enquanto a estrela e o planeta giram em torno do centro de massa do sistema estrela-planeta, a estrela se aproxima e se afasta de nós com a chamada velocidade ao longo da linha de visada, um movimento que pode ser detectado. A figura mostra o gráfico da velocidade ao longo da linha de visada em função do tempo para a estrela Herculis. Estima-se que a massa da estrela seja da massa do Sol. Supondo que apenas um planeta gira em torno da estrela e que a Terra está no plano da órbita do planeta, determine (a) a massa do planeta em unidades de , a massa de Júpiter, e (b) o raio de órbita do planeta em unidade o raio da órbita da Terra.
Passo 1
Show de bolinhas pessoal, tudo beleza com vocês?
Saca só, a situação parece complicada mas como a gente é malandro, vamos dar um jeitinho.
Primeiro podemos resumir ao que interessa: temos um par estrela-planeta orbitando o centro de massa do sistema formado pelo próprio par.
Isso é similar a um problema conhecido, o de um sistema binário de estrelas.
Para sistemas como esse, existe uma fórmula bastante chata de demonstrar (veja o livro didático!), é essa aqui:
Passo 2
Nessa fórmula, é a massa da estrela, que foi dada como sendo
Pois
Para completar a fórmula, vamos usar , e converter o período dado na questão para segundos:
O motivo pelo qual podemos usar é bem complicado. Pra resumir, aquele gráfico mostra a velocidade com que o corpo se move ao longo da nossa “linha de visão”, ou seja, ao longo do trajeto que vemos ele percorrer no “céu”.
O valor em torno do qual ele oscila é a velocidade que deve ser usada na fórmula. Cada “comprimento de onda” naquele gráfico é uma revolução completa da estrela, e por isso podemos usar aqueles dias como período de revolução.
Passo 3
Beleza, substituindo tudo isso na fórmula:
Essa fórmula vai resultar em uma equação do terceiro grau. O ideal seria resolvê-la em um computador, ou com algum método numérico.
O resultado vai ser .
E isso encerra a letra (a).
Passo 4
(b) Mais uma vez vamos precisar de uma fórmula pouco conhecida. Mas antes, veja essa ilustração da situação, fica bem mais fácil de entender quando temos a imagem:
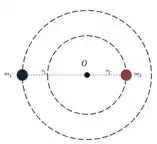
Em um sistema binário, onde dois corpos estão orbitando o centro de massa do par, se é a distância entre os centros dos corpos e é o raio de órbita do corpo mais externo (nesse caso, o planeta):
E vamos dizer que é o raio de órbita do corpo mais interno (nesse caso, a estrela):
Podemos então substituir uma fórmula na outra e achar:
Beleza. Como a questão quer o raio de órbita da estrela (), só precisamos achar o valor de .
Passo 5
Usando a velocidade na linha de visada para o planeta, podemos escrever:
E voltando na fórmula anterior:
Pronto!
Resposta
(a)
(b)