Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 15
Uma porta de 1,0 m de largura e 2,0 m de altura pesa 280 N e é suportada por duas dobradiças, uma situada a 0,50 m a partir do topo e a outra a 0,50 m a partir do ponto inferior. Cada dobradiça suporta metade do peso total da porta. Supondo que o centro de gravidade da porta esteja localizado em seu centro, ache o componente horizontal da força que cada dobradiça exerce sobre a porta.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma porta de de largura e de altura pesa e é suportada por duas dobradiças, uma situada a a partir do topo e a outra a a partir do ponto inferior.
Cada dobradiça suporta metade do peso total da porta.
Queremos encontrar a componente horizontal da força que cada dobradiça exerce sobre a porta dado que o centro de gravidade se encontra no centro da porta.
Para isso, vamos desenhar o diagrama de corpo livre para a porta e depois precisamos aplicar a primeira e a segunda condições de equilíbrio na porta.
Dessas condições, queremos dizer que o somatório das forças e dos torques são iguais a zero, ou seja:
Passo 2
Fazendo o diagrama de corpo livre, temos:
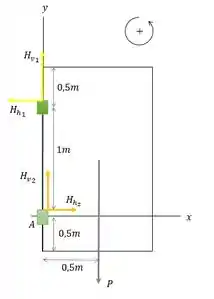
Sejam e as forças exercidas pelas dobradiças superior e inferior Vamos tomar a origem das coordenadas na dobradiça inferior (ponto A) e para cima.
Passo 3
Nos é dado que:
Agoa, basta aplicarmos a segunda lei de Newton no eixo horizontal:
Isso implica que:
Os componentes horizontais das forças da dobradiça são iguais em magnitude e oposto na direção.
Passo 4
Fazendo a soma dos torques no ponto A:
, e
têm braço de momento zero e, portanto, torque zero sobre um eixo em
este ponto.
Então:
E isso nos dá que:
Dessa forma, concluímos que:
Resposta
O componente horizontal de cada força de dobradiça é