Um carregador empurra uma mala de 20,0 kg para cima de uma rampa com inclinação de 25,0° acima da horizontal com uma força de módulo igual a 140 N que atua paralelamente à
rampa. O coeficiente de atrito cinético é dado por . Se a mala se desloca 3,80 m ao longo da rampa, calcule:
- o trabalho realizado sobre a mala pela força ;
- o trabalho realizado sobre a mala pela força gravitacional;
- o trabalho realizado sobre a mala pela força normal;
- o trabalho realizado sobre a mala pela força de atrito;
- o trabalho total realizado sobre a mala;
- se a velocidade da mala é nula na parte inferior da rampa, qual é sua velocidade depois que ela se desloca 3,80 m ao longo da rampa?
Passo 1
Opa! Aqui a gente ta empurrando uma mala de pra cima em uma rampa:
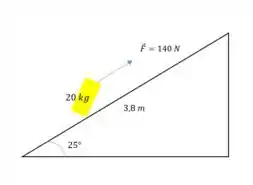
Temos que o coeficiente de atrito cinético é e a primeira coisa que a gente tem que calcular é o trabalho realizado sobre a mala pela força .
Bom galera, como se calcula o trabalho? Para a letra a:
Como nós temos a multiplicação dos dois vetores podemos usar o produto escalar:
Onde é o ângulo entre os vetores. Como a força e o deslocamento são vetores paralelos:
E sabendo que:
Só precisamos substituir:
Passo 2
Vamos para a b. Neste caso queremos o trabalho da força gravitacional. Esta força faz um ângulo de 90° com a horizontal, mas como nosso plano apresenta uma inclinação de 25°, nosso ângulo entre os vetores será:
Então:
Sando que a força peso é calculada como:
Aplicando no trabalho:
Passo 3
A letra c nos pede o trabalho da força normal. A força normal é perpendicular à superfície, consequentemente, forma um ângulo de 90° com a distância percorrida.
Ou seja:
Então:
E o trabalho:
Analisando a força de atrito, na letra d, temos que ele possui direção oposta ao deslocamento. Se é assim:
Então:
Neste caso, o trabalho será:
Sabendo que:
Como se lembram, não é?
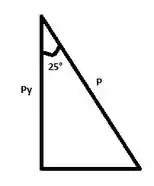
Então:
Agora já podemos calcular a força de atrito:
Substituímos tudo no trabalho:
Na equação do trabalho:
Passo 4
O trabalho total será a soma de todos os trabalhos calculados anteriormente:
Passo 5
Para a letra f precisamos achar a velocidade no topo da rampa. De acordo com o Teorema do Trabalho – Energia Cinética:
Como a velocidade no ponto inicial é zero, então a energia cinética neste ponto também é:
Se queremos a velocidade:
Substituímos nossos dados: