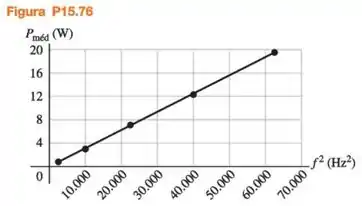
Você está medindo a dependência de frequência da potência média transmitida pelas ondas que trafegam em um fio. Em seu experimento, você usa um fio com densidade linear de 3,5 g/m. Para uma onda transversal no fio com amplitude de 4,0 mm, você mede (em watts) em função da frequência/ da onda (em Hz). Você escolheu desenhar em função de f2 (Figura P15.76). (a) Explique por que os valores de desenhados em função de f2 deverão estar bem ajustados a uma linha reta. (b) Use a inclinação da linha reta ajustada aos dados, mostrada na Figura P15.76, para calcular a velocidade das ondas. (c) Que frequência angular w resultaria em 10,0W?

A curva deve se aproximar de uma reta devido à natureza da equação referente à potência média, a qual se assemelha a uma função linear de 1º grau, considerando como sendo a variável pertencente ao eixo das abcissas. Como

Logo,

: inclinação da reta

Portanto, a curva da função referente à potência média da onda plotada no gráfico aproxima-se de uma reta devido à natureza de sua equação que corresponde a uma função linear de 1° grau.

(b) Para a resolução desta questão será utilizada a fórmula para o cálculo da potência média de uma onda em um fio, conforme no passo 1:

Com base nos dados fornecidos no gráfico, escolheu-se como ponto de referência o correspondente à potência média de 12,1 W (ponto mais exato para aferição dos dados):

Por ser uma reta, através de proporção, pode-se determinar o valor da frequência ao quadrado relativa a potência de 4 W (ponto arbitrário escolhido):

Sabe-se que a tangente do ângulo de inclinação de uma reta qualquer pode ser determinada conhecendo-se dois pontos pertencentes a tal reta a partir da expressão abaixo:

Para um melhor ajuste dos valores, considerou-se uma reta interligando o primeiro ponto da curva ao último ponto da curva . Logo, a tangente do ângulo de inclinação da reta corresponde a

A derivada da função correspondente a reta equivale a equação da potência média:

Como a derivada da função é numericamente igual à tangente do ângulo de inclinação, pode-se determinar o valor da tensão no fio a partir das seguintes operações abaixo:

Sabe-se também que a velocidade de propagação de uma onda em um fio é determinada pela seguinte expressão:

: velocidade

: tensão

: densidade linear

Com tais dados disponíveis, pode-se determinar a velocidade, conforme abaixo, faz-se a aproximação para dois algarismos significativos:

Portanto, a velocidade das ondas produzidas no fio corresponde a:

(c) Para a resolução desta questão será utilizada será utilizada a fórmula usada para a determinação da frequência angular:

: frequência angular

: frequência

Com base nos dados fornecidos no gráfico, verifica-se que a o valor da frequência ao quadrado relativa à potência média de 10 W equivale a 33,000 Hz²:

Determina-se então o valor final da frequência:

Assim, obtém-se a frequência angular conforme abaixo, faz-se a aproximação para dois algarismos significativos:

Logo, o valor da frequência angular correspondente a uma potência de 10 W equivale aproximadamente a: