Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.2 - Ex. 17
Você é membro de uma equipe de resgate nos Alpes. Você deve arremessar uma caixa de suprimentos de baixo para cima de uma encosta com ângulo de inclinação constante , de modo que chegue a um esquiador em apuros, que está a uma distância vertical acima da base da encosta. A encosta é escorregadia, mas há algum atrito presente, com coeficiente de atrito cinético . Use o teorema do trabalho-energia para calcular a velocidade escalar mínima que você deve imprimir à caixa na base da encosta, de modo que ela atinja o esquiador. Expresse sua resposta em termos de
Passo 1
Opa, bora resolver esse problema! Aqui temos que arremessar essa caixinha azul até o topo:
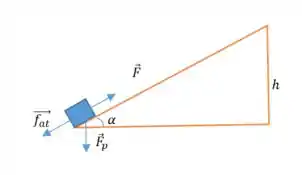
O atrito cinético é e devemos usar o teorema do trabalho-energia para calcular a velocidade inicial mínima pra que ela atinja o topo! Essa não vai ser uma resposta numérica, e precisamos expressar essa resposta em termos de
Antes de tudo vamos relembrar o que é o teorema trabalho – energia:
Onde é o trabalho total, é a energia cinética final e é a energia cinética inicial. Você deve ficar esperto aqui: sempre que falarmos em energia cinética, podemos falar de velocidade! Beleza? Agora vamos aplicar o teorema para esse problema, borá lá!
Passo 2
A velocidade escalar mínima é aquela que dá energia suficiente pra caixa subir até a altura , ou seja, na altura a velocidade da caixa deve ser nula. Assim a energia cinética final nesse ponto é zero. Vamos calcular o trabalho total. Ele vai ser dado pelo trabalho de duas forças: da força gravitacional e da força de atrito. Devemos calcular eles separadamente.
Trabalho da força gravitacional. Como a caixa sobe e a gravidade é vertical para baixo, então o ângulo entre a força e o deslocamento é de . O deslocamento é e a força peso é dada por . Então o trabalho realizado vai ser:
Passo 3
Agora o trabalho da força de atrito. A força de atrito é SEMPRE contrária ao movimento, então o ângulo entre ela e o deslocamento é . O deslocamento ao longo da colina vai ser . Lembrando que a força de atrito depende da força normal que nesse caso é , podemos calcular o trabalho realizado:
Assim o trabalho total vai ser a soma desses dois trabalhos:
Passo 4
E agora podemos usar o teorema para determinar a velocidade escalar inicial . Lembrando que a velocidade final deve ser zero, e que isso implica em energia final igual a zero, temos:
Dividindo tudo por e multiplicando a expressão por conseguimos isolar o valor de :
Taí a expressão pra velocidade inicial em termos das constantes dadas. Beleza? Vamos pra próxima?