Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 114

Se você pode atirar uma bola a uma distância horizontal máxima L, quando no nível do chão, a que distância você pode atirar a bola do alto de um edifício de altura h, se você a atira a (a) 0 ° , (b) 30 ° , (c) 45 ° ? Ignore a resistência do ar.)

Passo 1

E aí pessoal, beleza? Vamos lá resolver esse problema.

O enunciado nos propõe a seguinte situação descrita na figura abaixo. Quando mudamos o θ 0 , o alcance R também vai mudar e é exatamente isso que a questão quer.

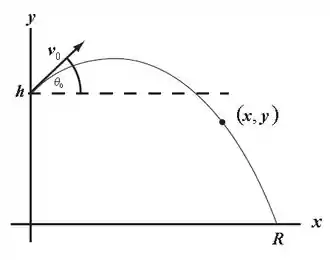
Vamos usar a equação da aceleração constante para expressar a posição horizontal da bola.

x = x 0 + v 0 x ⋅ t + 1 2 ⋅ a x ⋅ t 2

Onde:

  • a x = 0
  • x 0 = 0  
  • v 0 x = v 0 ⋅ cos ⁡ θ 0

Logo:

x = v 0 ⋅ cos ⁡ θ 0 ⋅ t

Temos também que:

y = y 0 + v 0 y ⋅ t - 1 2 ⋅ g ⋅ t 2

Onde:

  • y = h
  • y 0 = h
  • v 0 y = v 0 ⋅ sin ⁡ θ 0
  • g = 9,81   m / s 2

Logo:

h = h + v 0 ⋅ sin ⁡ θ 0 ⋅ t - 1 2 ⋅ 9,81 ⋅ t 2

Relacionando as duas equações do tempo encontradas, temos que:

0 = v 0 ⋅ sin ⁡ θ 0 ⋅ L v 0 ⋅ cos ⁡ θ 0 - 1 2 ⋅ 9,81 ⋅ L v 0 ⋅ cos ⁡ θ 0 2

0 = v 0 ⋅ tan ⁡ θ 0 ⋅ L - 1 2 ⋅ 9,81 ⋅ L v 0 ⋅ cos ⁡ θ 0 2

Mas sabemos que L = v 0 2 g sin ⁡ 2 θ 0 .

L = v 0 2 g sin ⁡ 2 ⋅ 45 ° = v 0 2 g

v 0 = g L

No momento do impacto, temos:

0 = x 0 + g L sin ⁡ θ 0 t v ô o - 1 2 ⋅ g ⋅ t v ô o 2

t v ô o = L g sin ⁡ θ 0 + sin 2 ⁡ θ 0 + 2

O alcance é dado por:

R = g L cos ⁡ θ 0 ⋅ t v ô o

R = g L cos ⁡ θ 0 ⋅ L g sin ⁡ θ 0 + sin 2 ⁡ θ 0 + 2

R = L cos ⁡ θ 0 sin ⁡ θ 0 + sin 2 ⁡ θ 0 + 2

Para θ 0 = 0 ° :

R = L cos ⁡ 0 sin ⁡ 0 + sin 2 ⁡ 0 + 2

R = L 2

Passo 2

Para θ 0 = 3 0 ° :

R = L cos ⁡ 3 0 sin ⁡ 3 0 + sin 2 ⁡ 3 0 + 2

R = L 3 2 1 2 + 1 4 + 2

R = L 3 2 1 2 + 3 2

R = L 3

Passo 3

Para θ 0 = 45 ° :

R = L cos ⁡ 45 sin ⁡ 45 + sin 2 ⁡ 45 + 2

R = L 2 2 2 2 + 2 4 + 2

R = L 2 2 2 2 + 10 2

R = L ⋅ 1,62

Resposta

a )   R = L 2

b )   R = L 3

c )   1,62 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma linha de montagem possui um grampeador que se desloca para a esquerda com 1,0 m/s enquanto as partes a serem grampeadas deslocam-se para a direita a 3,0 m/s. O grampeador insere 10 grampos por seg
Um dublê dirige um carro a 20 m/s em direção à beira de um penhasco de 30 m de altura. A estrada que leva ao penhasco é inclinada para cima em um ângulo de 20°.a. A que distância da base do penhasco o
Um gato está caçando um camundongo. Este corre em linha reta com velocidade de 1,5 m/s. Se o gato salta do piso em um ângulo de 30° e com rapidez igual a 4,0 m/s, de que distância atrás do camundongo
Você se encontra a 6,0m da parede de uma casa e deseja arremessar uma bola para seu colega que está a 6,0m da parede oposta. Tanto o arremesso acima do solo quanto a interceptação da bola ocorrem 1,0m
Os cavaleiros do rei Artur disparam um canhão do topo da muralha de um castelo. A bala de canhão é disparada com 50 m/s em um ângulo de 30º. Outra bala de canhão, que foi acidentalmente deixada cair,