Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 2.Problemas - Ex. 11
Você quer treinar para malabarista, mantendo duas bolas no ar, e suspendendo-as até uma altura máxima de 2m.
De quanto em quanto tempo e com que velocidade tem de mandar as bolas para cima?
Passo 1
Vamos analisar a situação
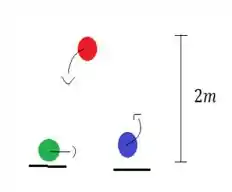
Nós queremos 2 bolas ao ar, então assim que a primeira bola chegar ao topo ( ) vamos jogar a segunda e enquanto ela estiver subindo a vermelha estará caindo. Tcharannn, 2 bolas ao ar!!
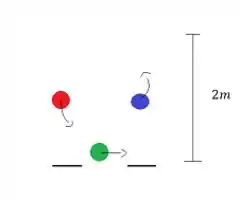
Assim que a vermelha cair a bola verde já estará na mão da direita prontinha pra ser jogada, exatamente quando a bola azul estiver no ponto máximo da trajetória, reiniciando o processo.
Visualizou agora? Haha, então responde aí e depois confere!
Passo 2
Vamos estabelecer os dados que a gente vai precisar
Como sempre que uma bola chegar à sua altura máxima a gente vai jogar outra, o intervalo entre as bolas vai ser justamente o tempo que a outra leva para subir 2 metros ! Opa, até aí tudo bem, mas... e a velocidade inicial, com que velocidade a gente vai jogar? A bola que tá lá em cima tem que cair na mão exatamente na mesma hora em que a do outro lado chega ao topo.
Aí que vem nosso pulo do gato, o tempo em que as duas bolas vão sofrer a aceleração da gravidade é o mesmo, então elas vão adquirir a mesma velocidade, só que uma vai ser quando a bola cai e a outra quando a bola é lançada!
Chega junto pra fazermos as contas:
Vamos achar a velocidade final que a bolinha pega quando cai na mão usando essa fórmula aqui :
Sabemos que , pois a bola parou ao chegar ao topo antes de começar a cair, e que . Então
Passo 3
Só nos resta achar o intervalo de tempo, para isso vamos usar a clássica equação