Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 20
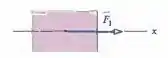
Existem duas forças horizontais atuando na caixa de da Fig. 5-39, mas a vista superior mostra apenas uma (de módulo ). A caixa se move ao longo do eixo . Para cada um dos valores da aceleração , da caixa, determine a segunda força em termos dos vetores unitários: (a), (b), (c), (d) e (e) .
Passo 1
Show de bolinhas pessoal, pra gente resolver essa questão, precisamos lembrar que a força resultante que age sobre um corpo é a soma de todas as forças que atuam no mesmo e está relacionada à aceleração pela definição da segunda lei de Newton:
Neste problema foi dado o módulo da força e o sentido, além disso, foi dado alguns valores de aceleração para que pudéssemos determinar o módulo da força .
Como o movimento é ao longo do eixo , usamos a lei de Newton para a componente :
Passo 2
Escrevendo a equação acima para nosso problema:
Substituindo os valores que são fixos:
Isolando o :
A partir dessa equação determinaremos todos os valores de substituindo os valores das acelerações.
Passo 3
Primeiro na letra (a), temos a aceleração , sendo assim obtemos que:
Agora na letra (b), a aceleração será dada como , de forma que:
E na letra (c), para obtemos:
Na letra (d), usando , temos:
Por fim mas não menos importante, temos na letra (e) a aceleração , portanto: