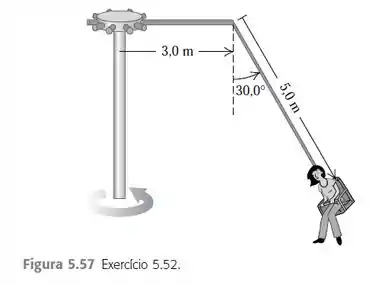
Um ‘balanço gigante’ de um parque de diversões consiste em um eixo vertical central com diversos braços horizontais ligados em sua extremidade superior (Figura 5.57). Cada braço suspende um assento por meio de um cabo de de comprimento, e a extremidade superior do cabo está presa ao braço a uma distância de do eixo central. a) Calcule o tempo para uma revolução do balanço quando o cabo que suporta o assento faz um ângulo de com a vertical. b) O ângulo depende do passageiro para uma dada taxa de revolução?
Passo 1
Show de bolinhas pessoal, bora lá analisar esse exercício!
Pelo enunciado, temos o seguinte ‘balanço gigante’ de um parque de diversões e suas medidas:
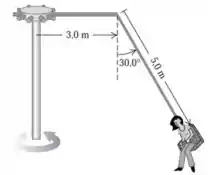
Queremos calcular o tempo para uma revolução do balanço quando o cabo que suporta o assento faz um ângulo de com a vertical.
Para isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando no corpo.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é massa e é a aceleração.
Fazendo isso a gente vai ver também se ângulo depende do passageiro para uma dada taxa de revolução.
Passo 2
Bom... aqui nós temos uma movimento circular e pela figura temos que o raio se dá por:
Temos também que é a força aplicada ao assento pela haste. Então, vamos esboçar o diagrama de corpo livre dessa situação:
Vamos aplicar a 2º Lei de Newton para a balança:
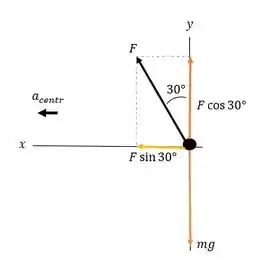
Como estamos em equilíbrio, vamos aplicar a 2º Lei de Newton no sistema para achar a velocidade e depois encontraremos o período.
Bora lá!
Passo 3
Olhando o diagrama, para o temos:
Onde é a aceleração da gravidade.
Passo 4
E para o :
Passo 5
Como temos um movimento circular, a aceleração centrípeta é dada por
Substituindo a aceleração em
Combinando estas duas equações e isolando
Agora que temos a velocidade, podemos achar o tempo!
Passo 6
- O período é dado por:
- A força resultante é proporcional a em e a massa se divide e o ângulo para uma determinada taxa de rotação é independente da massa dos passageiros.
Onde é a velocidade.
Passo 7
Resposta
- Não.