Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 07

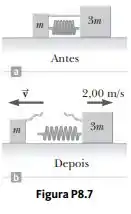
Dois blocos de massas m e 3 m são colocados em uma superfície horizontal sem atrito. Uma mola leve é atada ao bloco de maior massa e os blocos são empurrados juntos com a mola entre eles (Fig. P8.7). Uma corda que inicialmente mantinha os blocos juntos é queimada; depois disso, o bloco de massa 3 m move-se para a direita com uma velocidade de 2,00   m / s . (a) Qual é a velocidade do bloco de massa m? (b) Encontre a energia potencial elástica original do sistema, considerando m   =   0,350   k g . (c) A energia original está na mola ou na corda? (d) Explique sua resposta à parte (c). (e) O momento do sistema é conservado no processo de queima-separação? Explique como isso é possível considerando que (f) há grandes forças agindo, e (g) não há movimento anterior nem muito movimento posteriormente.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Para o sistema de dois blocos Δ p = 0 ,   ou  p i = p f . Portanto,

0 = m v m + 3 m 2.00 m s

v m = - 6.00 m s   ( m o v i m e n t o   p a r a   a   e s q u e r d a ) .

Passo 2

Letra b:

1 2 k x 2 = 1 2 m v M 2 + 1 2 ( 3 m ) v 3 M 2 = 1 2 ( 0.350 k g ) ( - 6.00 m / s ) 2 + 3 2 ( 0.350 k g ) ( 2.00 m / s ) 2 = 8.40 J

Passo 3

Letra c:

A energia original está na mola.

Passo 4

Letra d:

Uma força teve que ser exercida sobre um deslocamento para comprimir a mola, transferindo energia para ela pelo trabalho. A corda exerce força, mas sem deslocamento.

Passo 5

Letra e:

O momento do sistema é conservado com o valor zero.

Passo 6

Letra f:

As forças nos dois blocos são forças internas, que não podem mudar a dinâmica do sistema. Então, o sistema é isolado.

Passo 7

Letra g:

Mesmo que haja administração depois, os momentos finais são de magnitude igual em direções opostas, então o momento final do sistema ainda é zero.

Resposta

  1. - 6.00 m s
  2. 8.40 J
  3. A energia original está na mola.
  4. Uma força teve que ser exercida sobre um deslocamento para comprimir a mola, transferindo energia para ela pelo trabalho. A corda exerce força, mas sem deslocamento.
  5. O momento do sistema é conservado com o valor zero.
  6. As forças nos dois blocos são forças internas, que não podem mudar a dinâmica do sistema. Então, o sistema é isolado.
  7. Mesmo que haja administração depois, os momentos finais são de magnitude igual em direções opostas, então o momento final do sistema ainda é zero.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

126- A partícula 1, com massa de 200 g, que se move a uma velocidade de 3,00 m/s, sofre uma colisão unidimensional com a partícula 2, com massa de 400 g, que estava inicialmente em repouso. Qual é o m
123- Uma sonda espacial não tripulada (de massa m e velocidade v em relação ao Sol) se aproxima do planeta Júpiter (de massa M e velocidade V J em relação ao Sol), como mostra a Fig. 9-84. A sonda con
Um vagão de trem de 10000k g desloca-se a 2,0m / s quando uma carga de 4000k g de cascalho subitamente cai dentro do mesmo. Qual é a velocidade do vagão logo após a carga de cascalho ter caído dentro
Um vagão aberto de trem 5000 kg desloca-se sem atrito sobre os trilhos a 22 m/s quando começa a chover torrencialmente. Alguns minutos mais tarde, a velocidade do vagão baixou para 20 m/s. Qual é a ma
O nêutron é uma partícula subatômica eletricamente neutra com uma massa ligeiramente maior do que a do próton. Qualquer nêutron livre é radioativo e decai, após decorridos alguns minutos, em outras pa