Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 11.Problemas - Ex. 50
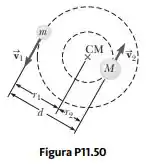
Duas estrelas de massa e , separadas por uma distância , movem-se em órbitas circulares em torno de seus centros de massa (Fig. P). Mostre que cada estrela tem um período determinado por . Prossiga como segue: Aplique a Segunda Lei de Newton a cada estrela. Note que a condição de centro de massa requer que , em que .
Passo 1
Vem comigo que a gente detona essa juntos!
O enunciado já nos diz o que devemos fazer que é usar a segunda lei de Newton, mas por quê?
O período é dado por:
Então vamos usar essa segunda lei para encontrar uma expressão para a velocidade já que a expressão que queremos chegar não depende dela.
Como temos movimentos circulares a força resultante dada pela força gravitacional nesse caso é igual a força centrípeta, assim:
Onde é a distância entre as estrelas que interagem.
Como as estrelas giram sempre separadas com a mesma distância elas tema mesma velocidade .
Passo 2
Primeiro vamos fazer a análise para a estrela de massa , temos:
Agora vamos fazer para a estrela de massa , assim:
Agora vamos somar as duas expressões que encontramos, assim:
Usando que , temos:
Passo 3
Agora vamos encontrar , temos:
Substituindo o que temos para ficamos com:
Prontinho, chegamos aonde ele queria!
Resposta
Demonstrado acima.