Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.7 - Ex. 33

O bloco na Fig. 7-9a está sobre uma superfície horizontal sem atrito e a constante elástica é 50   N / m . Inicialmente, a mola está relaxada e o bloco está parado no ponto x   = 0 . Uma força com módulo constante de 3,0   N é aplicada ao bloco, puxando-o no sentido positivo do eixo x e alongando a mola até o bloco parar. Quando este ponto é atingido, qual é (a) a posição do bloco, (b) o trabalho realizado sobre o bloco pela força aplicada e (c) o trabalho realizado sobre o bloco pela força elástica? Durante o deslocamento do bloco, qual é (d) a posição do bloco na qual a energia cinética é máxima e (e) o valor desta energia cinética máxima?

Passo 1

Então galera , nós sabemos que :

W = F x cos ⁡ 0 ° = F x

W = k x 2 2

Sendo assim , temos que :

F x = k x 2 2

3 N x = 50 N m x 2 2

o que nos dá uma única solução diferente de zero ,   x   =   ( 3,0 / 25 )   m   =   0,12   m .

Passo 2

O trabalho realizado pela força aplicada , por sua vez é dado pela relação :

W a   =   F x   =   ( 3,0   N ) ( 0,12   m )   =   0,36   J

Passo 3

Bom pessoal nós sabemos que o trabalho realizado pela mola percorre a mesma distância e na mesma direção do trabalho realizado pela força aplicada , porém sentidos opostos . Sendo assim :

W s   =   - W a = - 0,36 J  

.

Passo 4

Então galera , considerando K f = K   e K i = 0 , dessa forma , obtemos que :

K = F x - k x 2 2

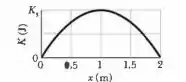
Para acharmos o ponto x = x c onde a energia cinética K é máxima , devemos derivar K em relação a x e igualar a equação que acharmos a zero . Sendo assim :

x c = F k = 3 50 m = 0,060 m

Note que x c   também é o ponto no qual a força resultante é nula.

Passo 5

Agora podemos substituir o valor de x = x c na expressão da energia cinética para obtermos a energia cinética máxima .Sendo assim :

K m á x = k x c 2 2 = 50 N m 0,06 m 2 2

K m á x   =   0,090   J

Resposta

W a = 0,36   J

W s = - 0,36   J

x c = 0,060   m

K m á x = 0,090   J

Tranquilo galera??? Bora resolver mais questões então!!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador harmônico tridimensional isotrópico é definido como uma partícula que se move sob a ação de forças associadas à energia potencial U x , y , z = 1 2 k ( x 2 + y 2 + z 2 ) Onde k é uma cons
Uma partícula está confinada a mover-se no semi-espaço z ≥0 , sob a ação de forças conservativas, de energia potencial U x , y , z = F 0 z + 1 2 k x 2 + y 2 , onde F 0ek são positivas. a) Calcule as c
Uma estrutura rígida triangular é construída com três hastes iguais e seu plano é vertical, com a base horizontal. Nos dois outros lados estão enfiadas duas bolinhas idênticas de massa m, atravessadas
Num parque de diversões, um carrinho desce de uma altura h para dar a volta no loop de raio R indicado na figura. a) Desprezando o atrito do carrinho com o trilho, qual menor valor h 1 de altura neces
Um garotinho esquimó desastrado escorrega do alto do seu iglu, um domo esférico de gelo de 3m de atura. a) De que altura acima do solo ele cai? b) A que distância da parede do iglu ele cai?