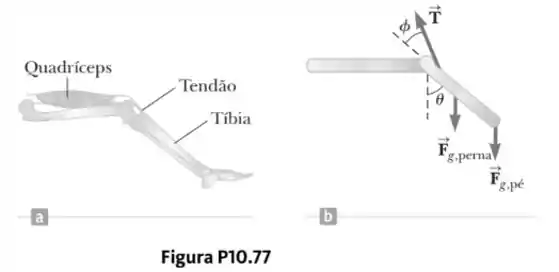
O grande músculo quadríceps na parte superior da perna termina em sua extremidade inferior em um tendão ligado à extremidade superior da tíbia (Fig. P10.77a). As forças sobre a parte inferior da perna quando esta é estendida são modeladas como na Figura P10.77b, onde   é a força no tensão, é a força gravitacional agindo sobre a parte inferior da perna e é a força gravitacional agindo sobre o pé. Encontre quando o tendão está em um ângulo de com a tíbia, supondo , e a perna estendida em um ângulo com relação à vertical. Suponha também o centro de gravidade da tíbia está em seu centro geométrico e o tendão ligado à parte inferior da perna em uma posição um quinto para baixo na perna.

Passo 1

Resposta